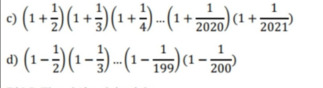6.7:
Ta có: \(A=\frac{17^{18}+1}{17^{19}+1}<1\)
\(A=\frac{17^{18}+1}{17^{19}+1}<\frac{17^{18}+1+16}{17^{19}+1+16}=\frac{17^{18}+17}{17^{19}+17}=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=B\)
\(\Rightarrow A< B\)
6.8: tương tự
6.7 *
Ta có : \(\dfrac{a}{b}< 1\)
A = \(\dfrac{17^{18}+1}{17^{19}+1}< \dfrac{17^{18}+1+16}{17^{19}+1+16}=\dfrac{17^{18}+17}{17^{19}+17}=\dfrac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=\dfrac{17^{17}+1}{17^{18}+1}=\)B
6.7*
Ta có : \(\dfrac{a}{b}< 1\)
A= \(\dfrac{17^{18}+1}{17^{19}+1}< \dfrac{17^{18}+1+16}{17^{19}+1+16}=\dfrac{17^{18}+17}{17^{19}+17}=\dfrac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=\dfrac{17^{17}+1}{17^{18}+1}=B\)
Vậy A < B
\(\dfrac{a}{b}< 1\Leftrightarrow\dfrac{a+m}{b+m}< 1\left(m\in N\right)\)
\(\Leftrightarrow A=\dfrac{17^{18}+1}{17^{19}+1}< 1\)
\(\Leftrightarrow\dfrac{17^{18}+1}{17^{19}+1}< \dfrac{17^{18}+1+16}{17^{19}+1+16}< \dfrac{17^{18}+17}{17^{19}+17}< \dfrac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}< \dfrac{17^{17}+1}{17^{18}+1}=B\)\(\Leftrightarrow A< B\)
\(\dfrac{a}{b}>1\Leftrightarrow\dfrac{a+m}{b+m}>1\left(m\in N\right)\)
\(\Leftrightarrow C=\dfrac{98^{99}+1}{98^{89}+1}>1\)
\(\Leftrightarrow C>\dfrac{98^{99}+1+97}{98^{89}+1+97}>\dfrac{98^{99}+98}{98^{89}+98}>\dfrac{98\left(98^{98}+1\right)}{98\left(88^{88}+1\right)}>\dfrac{98^{98}+1}{98^{88}+1}=D\)\(\Leftrightarrow C>D\)