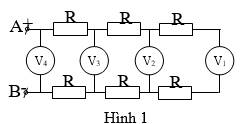
\(I_{V1}=\dfrac{U_1}{R_V};I_{V2}=\dfrac{U_2}{R_V};I_{V3}=\dfrac{U_3}{R_V}\)
\(U_2=\left(2R+R_V\right)I_{V1}=\left(2R+R_V\right)\cdot\dfrac{U_1}{R_V}=U_1\left(\dfrac{2R}{R_V}+1\right)\Leftrightarrow\dfrac{R}{R_V}=\dfrac{\dfrac{U_2}{U_1}-1}{2}\left(1\right)\)
\(U_3=2R\left(I_{V1}+I_{V2}\right)+U_2=2R\left(\dfrac{U_1+U_2}{R_V}\right)+U_2=\dfrac{R}{R_V}\cdot2\left(U_1+U_2\right)+U_2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow U_3=\left(\dfrac{U_2}{U_1}-1\right)\left(U_1+U_2\right)+U_2\)
thay số ta được: \(5=\left(U_2-1\right)\left(U_2+1\right)+U_2=U^2_2+U_2-1\Leftrightarrow U^2_2+U_2-6=0\Leftrightarrow\left[{}\begin{matrix}U_2=2V\\U_2=-3\left(loại\right)\end{matrix}\right.\)
\(U_4=2R\left(I_{V1}+I_{V2}+I_{V3}\right)+U_3\)
\(\Leftrightarrow U_4=\dfrac{2R}{R_V}\left(U_1+U_2+U_3\right)+U_3\)
\(\Leftrightarrow U_4=\left(\dfrac{U_2}{U_1}-1\right)\left(U_1+U_2+U_3\right)+U_3\)
\(\Leftrightarrow U_4=\left(2-1\right)\left(1+2+5\right)+5=13V\)
Chương I- Điện học
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
4.1. Cho mạch điện như hình 3, các điện trở R có giá trị bằng nhau và các vôn kế có điện trở bằng nhau. Biết vôn kế V1 chỉ 1V, vôn kế V3 chỉ 5V. Tìm số chỉ của các vôn kế V2 và V4.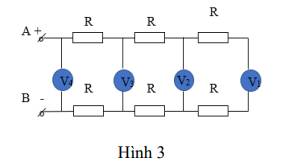
Hai vôn kế giống nhau, mỗi cái có điện trở R, được mắc với một điện trở R rồi mắc vào một nguồn có hiệu điện thế U không đổi như hình bên. Biết một trong hai vôn kế chỉ 6,2 V, vôn kế còn lại chỉ 2,8 V. a) Tính U. Hỏi vôn kế nào chỉ 6,2 V, vôn kế nào chỉ 2,8 V? b) Tính tỉ số Rv/ R c) Tháo vôn kế V2 ra khỏi mạch thì vôn kế V1 chỉ bao nhiêu?
Cho mạch điện như hình vẽ.Hiệu điện thế giữa 2 đầu đoạn mạch bằng U180V. R12000Ω, R23000Ω.a, Khi mắc vôn kế có điện trở Rv song song với R1 thì vôn kế chỉ U160V. Hãy xác định cường độ dòng điện qua các điện trở R1 và R2.b, Nếu mắc vôn kế song song với điện trở R2 thì vôn kế chỉ bao nhiêu?
Đọc tiếp
Cho mạch điện như hình vẽ.Hiệu điện thế giữa 2 đầu đoạn mạch bằng U=180V. R1=2000Ω, R2=3000Ω.
a, Khi mắc vôn kế có điện trở Rv song song với R1 thì vôn kế chỉ U1=60V. Hãy xác định cường độ dòng điện qua các điện trở R1 và R2.
b, Nếu mắc vôn kế song song với điện trở R2 thì vôn kế chỉ bao nhiêu?
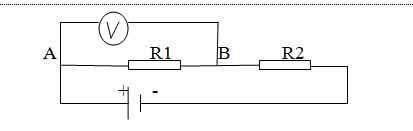
Một mạch điện gồm 1 ampe kế có điện trở Ra,1điện trở R=10Ω và 1 vôn kế có điện trở Rv=1000V,mắc nối tiếp.Đặt vào 2 đầu đoạn mạch 1 hiệu điện thế U thì số chỉ của vôn kế là 100V.Nếu mắc vôn kế song song với R thì số chỉ của nó vẫn là 100V.Tính Ra và U
Cho mạch điện như hình 8. R1 = R2 = R3 = 6Ω ; R4 = 4Ω ; UAB = 18V. Vôn kế có điện trở vô cùng lớn.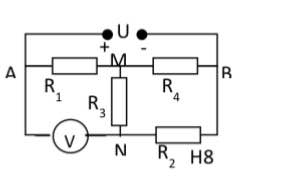
a. Tìm số chỉ vôn kế.
b. Tháo vôn kế ra khỏi mạch và mắc vào vị trí
đó một ampe kế có điện trở rất nhỏ. Tìm số chỉ
của ampe kế và chiều dòng điện qua ampe kế.
Cho mạch điện. Ampe kế A2 chỉ 2A, các điện trở có giá trị là: 1W, 2W, 3W, 4W nhưng chưa biết vị trí của chúng trong mạch điện. Xác định vị trí các điện trở đó và số chỉ ampe kế A1. Biết vôn kế V chỉ 10V và số chỉ các ampe kế là số nguyên. Các dụng cụ đo là lý tưởng.
cho ba điện trở có giá trị lần lượt là R,2R và 3R mắc nối tiếp với nhau vào cùng một hiệu điện thế không đổi.Dùng một vôn kế(có điện trở là Rv) để đo lần lượt hiệu điện thế giữa hai đầu điện trở R và 2R thì được các trị số U1=40,6V và U2=72,5V.Nếu mắc vôn kế này vào hai đầu điện trở 3R thì vôn kế này chỉ bao nhiêu?
Cho sơ đồ mạch điện như hình vẽ.
R1=R3=R4=4Ω, R2=2Ω, U=6v.
a, Khi nối A và D 1 vôn kế thì vôn kế chỉ bao nhiêu? Biết điện trở vôn kế rất lớn.
b, Khi nối A và D 1 ampe kế thì ampe kế chỉ bao nhiêu?Biết điện trở ampe kế rất nhỏ.

Cho mạch điện như hình vẽ: Biết UAB 10V không đổi, vôn kế có điện trở rất lớn. R1 4; R2 8 ; R3 10; R4 là một biến trở đủ lớn. a) Biết vôn kế chỉ 0 V. Tính R4. b) Biết UCD 2V. Tính R4 . c) Thay vôn kế bằng ampe kế A có điện trở không đáng kể, dòng điện chạy qua ampe kế có chiều từ C đến D. Tính R4 để số chỉ của ampe kế là 400 mA. d, Thay Ampe kế A bằng Ampe kế A1 có điện trở RA1 1Ω với R4 6Ω tìm số chỉ của Ampe kế A1 và cho biết chiều dòng điện chạy qua A
Đọc tiếp
Cho mạch điện như hình vẽ: Biết UAB = 10V không đổi, vôn kế có điện trở rất lớn. R1 = 4; R2 = 8 ; R3 = 10; R4 là một biến trở đủ lớn. a) Biết vôn kế chỉ 0 V. Tính R4. b) Biết UCD = 2V. Tính R4 . c) Thay vôn kế bằng ampe kế A có điện trở không đáng kể, dòng điện chạy qua ampe kế có chiều từ C đến D. Tính R4 để số chỉ của ampe kế là 400 mA. d, Thay Ampe kế A bằng Ampe kế A1 có điện trở RA1= 1Ω với R4 = 6Ω tìm số chỉ của Ampe kế A1 và cho biết chiều dòng điện chạy qua A