Violympic toán 9
Các câu hỏi tương tự
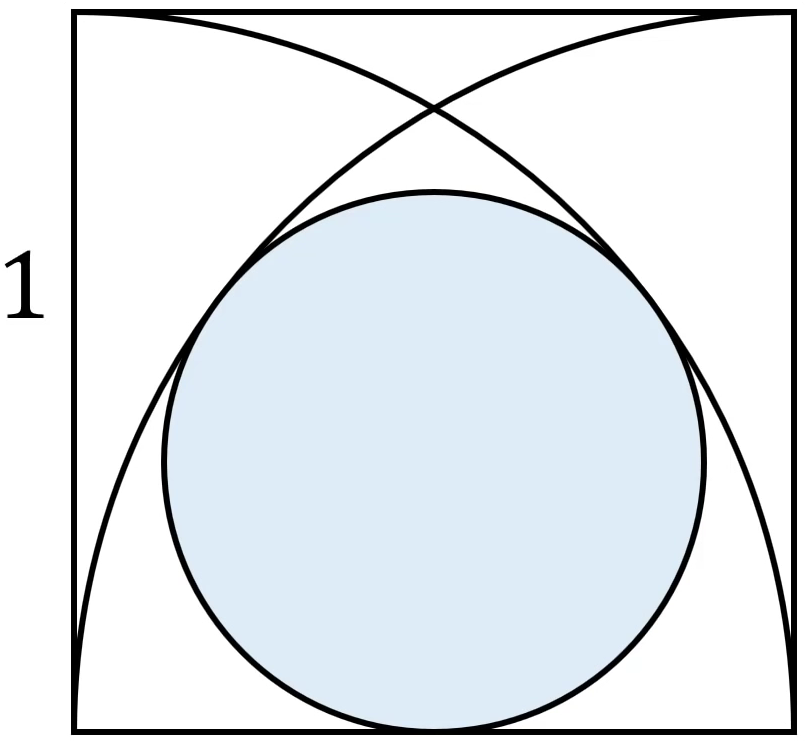
Cho hình vuông cạnh bằng 1, dựng hai phần tư đường tròn và đường tròn tiếp xúc với các phần tư, cạnh hình vuông như hình vẽ.
Tính bán kính hình tròn màu xanh.
cho đường tròn (O) đường kính EF, D là điểm di chuyển trên đường tròn (O) (D khác E và F). kẻ DK vuông góc với EF tại K(K thuộc EF). gọi M là hình chiếu vuông góc của K lên DE. Gọi N là hình chiếu vuông góc của K lên DF
Nhờ vẽ hình
Cho đường tròn tâm O bán kính R và đường thẳng(Δ)không có điểm chung với đường tròn tâm( O), H là hình chiếu vuông góc của O trên (Δ) .từ điểm M bất kì trên (Δ) ( M không trùng H), vẽ 2 tiếp tuyến MA, MB với đường tròn (O) (A,B là hai tiếp điểm ).Gọi I, K theo thứ tự là giao điểm của AB với OM và OH1. Chứng minh AB 2 .AK với 5 điểmM ,A ,O, B, H cùng thuộc đường tròn2 .Chứng minh OI.OH OK.OM R^23.trên đoạn OA lấy điểm N sao cho AN 2ON. đường trung trực của BN cắt OM ở E .tính tỉ sốdfrac{OE}{O...
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng(Δ)không có điểm chung với đường tròn tâm( O), H là hình chiếu vuông góc của O trên (Δ) .từ điểm M bất kì trên (Δ) ( M không trùng H), vẽ 2 tiếp tuyến MA, MB với đường tròn (O) (A,B là hai tiếp điểm ).Gọi I, K theo thứ tự là giao điểm của AB với OM và OH
1. Chứng minh AB = 2 .AK với 5 điểmM ,A ,O, B, H cùng thuộc đường tròn
2 .Chứng minh OI.OH = OK.OM = \(R^2\)
3.trên đoạn OA lấy điểm N sao cho AN = 2ON. đường trung trực của BN cắt OM ở E .tính tỉ số\(\dfrac{OE}{OM}\)
Cho nửa đường tròn (O;R) đường kính AB. Trên nửa mặt phẳng bờ AB có chứa nửa đường tròn vẽ tiếp tuyến Ax với nửa đường tròn, trên Ax lấy M sao cho AMR. Từ M vẽ tiếp tuyến MC với nửa đường tròn, từ C vẽ CH vuông góc với AB,CE vuông góc với AM. Đường thẳng vuông góc với AB tại O cắt BC tại N.Đường thẳng MO cắt CE,CA,CH lần lượt tạiQ,K,P.a ) MB cắt CH tại I. Chứng minh KI song song vớiAB b) Gọi G và F lần lượt là trung điểm của AH và AE. Chứng minh PG vuông góc với QF
Đọc tiếp
Cho nửa đường tròn (O;R) đường kính AB. Trên nửa mặt phẳng bờ AB có chứa nửa đường tròn vẽ tiếp tuyến Ax với nửa đường tròn, trên Ax lấy M sao cho AM>R. Từ M vẽ tiếp tuyến MC với nửa đường tròn, từ C vẽ CH vuông góc với AB,CE vuông góc với AM. Đường thẳng vuông góc với AB tại O cắt BC tại N.Đường thẳng MO cắt CE,CA,CH lần lượt tạiQ,K,P.a ) MB cắt CH tại I. Chứng minh KI song song vớiAB b) Gọi G và F lần lượt là trung điểm của AH và AE. Chứng minh PG vuông góc với QF
Bài toán. Cho nửa đường tròn tâm O đường kính AB. Gọi C là điểm nằm trên nửa đường tròn (C khác A, B). Gọi H là hình chiếu vuông góc của C trên AB; D là điểm đổi xứng với A qua C; I là trung điểm CH; J là trung điểm DH.a) Chứng minh $angle CIJangle CBH$ (đã làm)b) Chứng minh tam giác CJH đồng dạng với HIB (đã làm)c) Gọi E là giao điểm của HD và BI. Chứng minh $HEcdot HDHC^2.$d) Xác định vị trí của điểm C trên nửa đường tròn để $AH+CH$ đạt Max.Ps: Chán hoc24 phiên bản mới ghê, em đăng câu hỏi hơi...
Đọc tiếp
Bài toán. Cho nửa đường tròn tâm O đường kính AB. Gọi C là điểm nằm trên nửa đường tròn (C khác A, B). Gọi H là hình chiếu vuông góc của C trên AB; D là điểm đổi xứng với A qua C; I là trung điểm CH; J là trung điểm DH.
a) Chứng minh $\angle CIJ=\angle CBH$ (đã làm)
b) Chứng minh tam giác CJH đồng dạng với HIB (đã làm)
c) Gọi E là giao điểm của HD và BI. Chứng minh $HE\cdot HD=HC^2.$
d) Xác định vị trí của điểm C trên nửa đường tròn để $AH+CH$ đạt Max.
Ps: Chán hoc24 phiên bản mới ghê, em đăng câu hỏi hơi dài (do có những thảo luận) mà hoc24 tự ý rút gọn làm mất nội dung câu hỏi. Đăng ảnh thì không hiển thị. Em phải đăng lại lần này là lần thứ 3.
cho đường tròn (O) đường kính EF, D là điểm di chuyển trên đường tròn (O) (D khác E và F). kẻ DK vuông góc với EF tại K(K thuộc EF). gọi M là hình chiếu vuông góc của K lên DE. Gọi N là hình chiếu vuông góc của K lên DF
a.cm tứ giác EMNF nội tiếp
b.cm DM.DE=DN.DF
Cho đường tròn (O) đường kính EF, D là điểm di chuyển trên đường tròn (O) (D khác E và F). Kẻ DK vuông góc với EF tại K (K thuộc EF). Gọi M là hình chiếu vuông góc của K lên DE. Gọi N là hình chiếu vuông góc của K lên DF.a. Chứng minh tứ giác EMNF nội tiếpb. Chứng minh DM.DE DN.DFc. Tìm vị trí của điểm D sao cho bán kính đường tròn ngoại tiếp tam giác EFM đạt giá trị lớn nhất.
Đọc tiếp
Cho đường tròn (O) đường kính EF, D là điểm di chuyển trên đường tròn (O) (D khác E và F). Kẻ DK vuông góc với EF tại K (K thuộc EF). Gọi M là hình chiếu vuông góc của K lên DE. Gọi N là hình chiếu vuông góc của K lên DF.
a. Chứng minh tứ giác EMNF nội tiếp
b. Chứng minh DM.DE = DN.DF
c. Tìm vị trí của điểm D sao cho bán kính đường tròn ngoại tiếp tam giác EFM đạt giá trị lớn nhất.
Cho đường tròn (O) đường kính EF, D là điểm di chuyển trên đường tròn (O) (D khác E và F). Kẻ DK vuông góc với EF tại K (K thuộc EF). Gọi M là hình chiếu vuông góc của K lên DE. Gọi N là hình chiếu vuông góc của K lên DF.
a. Chứng minh tứ giác EMNF nội tiếp
cho nửa đường tròn tâm O đường kính BC.Điểm A thuộc nửa đường tròn tâm O khác B và C.Kẻ AH vuông góc BC (H inBC). Trên nửa mặt phẳng bờ BC chứa A vẽ nửa đường tròn tâm I đường kính BH và nửa đường tròn tâm K đường kính CH , chúng lần lượt cắt AB , AC ở D và E. a,Chứng minh: tứ giác BCED nội tiếpb,Gọi M,N lần lượt là các điểm đối xứng H qua AB và AC.Chứng minh MN là tiếp tuyến của nửa đường tròn tâm Oc,Biết BC50 cm , DE20 cm .Tính diện tích hình được giới hạn bởi 3 nửa đường tròn tâm O,I,K
Đọc tiếp
cho nửa đường tròn tâm O đường kính BC.Điểm A thuộc nửa đường tròn tâm O khác B và C.Kẻ AH vuông góc BC (H \(\in\)BC). Trên nửa mặt phẳng bờ BC chứa A vẽ nửa đường tròn tâm I đường kính BH và nửa đường tròn tâm K đường kính CH , chúng lần lượt cắt AB , AC ở D và E.
a,Chứng minh: tứ giác BCED nội tiếp
b,Gọi M,N lần lượt là các điểm đối xứng H qua AB và AC.Chứng minh MN là tiếp tuyến của nửa đường tròn tâm O
c,Biết BC=50 cm , DE=20 cm .Tính diện tích hình được giới hạn bởi 3 nửa đường tròn tâm O,I,K









