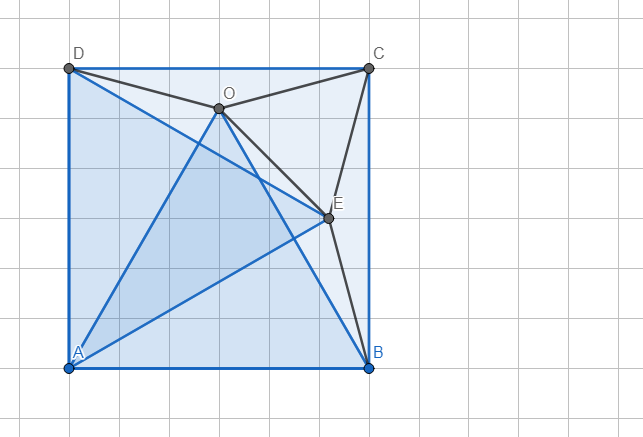
*Dựng △ADE đều.
\(\widehat{ODC}=\widehat{OCD}=15^0\Rightarrow\)△DOC cân tại O.
\(\Rightarrow OD=OC;\widehat{DOC}=180^0-2\widehat{ODC}=180^0-2.15^0=150^0\)
\(\widehat{BAE}=\widehat{CDE}=90^0-\widehat{ADE}=90^0-60^0=30^0\)
\(AB=AE=DE=DC=AD\).
\(\Rightarrow\)△DCE cân tại D, △ABE cân tại A.
\(\Rightarrow\widehat{DCE}=\widehat{ABE}=\dfrac{180^0-\widehat{BAE}}{2}=\dfrac{180^0-30^0}{2}=75^0\).
\(\Rightarrow\widehat{ECB}=\widehat{EBC}=90^0-\widehat{DCE}=90^0-75^0=15^0\)
\(\widehat{OCE}=90^0-\widehat{OCD}-\widehat{BCE}=90^0-15^0-15^0=60^0\)
△DOC và △BEC có: \(\widehat{ODC}=\widehat{EBC}=15^0;\widehat{OCD}=\widehat{ECB}=15^0;DC=BC\)
\(\Rightarrow\)△DOC=△BEC (g-c-g)
\(\Rightarrow OD=BE=OC=EC\)
\(\Rightarrow\)△OCE cân tại C mà \(\widehat{OCE}=60^0\)
\(\Rightarrow\)△OCE đều.
\(\widehat{OEB}=360^0-\widehat{OEC}-\widehat{BEC}=360^0-60^0-150^0=150^0\)
\(OE=CE=EB\Rightarrow\)△OEB cân tại E.
\(\Rightarrow\widehat{OBE}=\dfrac{180^0-\widehat{OEB}}{2}=\dfrac{180^0-150^0}{2}=15^0\)
\(\widehat{OBA}=90^0-\widehat{OBE}-\widehat{CBE}=90^0-15^0-15^0=60^0\)
Mà △OAB cân tại O \(\Rightarrow\)△OAB đều.










