§1. Các định nghĩa
Các câu hỏi tương tự
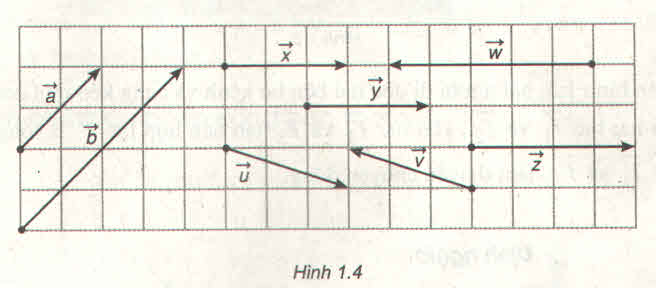
Trong hình 1.4 hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau :
Cho hình bình hành ABCD. Gọi E F M N , , , lần lượt là trung điểm AB BC CD DA , , , .
Chứng minh rằng
a) Ba vectơ EF AC MN , , cùng phương;
| b) | . Suy ra: EFMN là hình bình hành |
EF NM
Cho hình bình hành ABCD có O = AC n BD a,Tìm các vectơ khác vectơ O + Cùng phương với vectơ OA + Cùng chiều với vectơ BD b, Tìm các vectơ + bằng với AB + bằng với CO
: Cho hình thang vuông ABCD vuông ở A và D, AB = AD = a, góc C bằng 45 độ . Tính độ dài. các vec tơ CD, BD, CB, AC
Cho hình bình hành ABCD, tâm O. Hãy chỉ ra:
- các vectơ cùng hướng với vectơ OB
- các vectơ ngược hướng với vectơ OA
- các vectơ bằng nhau với vectơ OC
giúp mình nha, cảm ơn nhiều ^-^
Cho ba vectơ overrightarrow{a},overrightarrow{b},overrightarrow{c} đều khác overrightarrow{0}. Các khẳng định sau đúng hay sai ?
a) Nếu hai vectơ overrightarrow{a},overrightarrow{b} cùng phương với overrightarrow{c} thì overrightarrow{a} và overrightarrow{b} cùng phương
b) Nếu overrightarrow{a}, overrightarrow{b} cùng ngược hướng với overrightarrow{c} thì overrightarrow{a} và overrightarrow{b} cùng hướng
Đọc tiếp
Cho ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đều khác \(\overrightarrow{0}\). Các khẳng định sau đúng hay sai ?
a) Nếu hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) cùng phương với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng phương
b) Nếu \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng ngược hướng với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng hướng
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) overrightarrow{AB} và overrightarrow{AC} cùng hướng, left|overrightarrow{AB}right|left|overrightarrow{AC}right|
b) overrightarrow{AB} và overrightarrow{AC} ngược hướng
c) overrightarrow{AB} và overrightarrow{AC} cùng phương
Đọc tiếp
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng hướng, \(\left|\overrightarrow{AB}\right|>\left|\overrightarrow{AC}\right|\)
b) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ngược hướng
c) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương
Cho tứ giác hình bình hành tâm O. Hãy chỉ ra các vectơ :
+ cùng hướng với vectơ OB + ngược hướng với vectơ OA + Bằng nhau với vectơ OC Giúp mình nha, cảm ơn nhiều ^_^Cho hình vuông ABCD tâm O. Liệt kê tất cả các vectơ bằng nhau (khác \(\overrightarrow{0}\)) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối ?







