Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
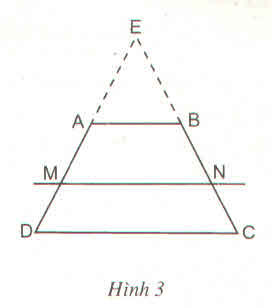
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh











