Cho hình hộp ABCD.A'B'C'D'
a) Trong mặt phẳng (ABCD), tìm vectơ hiệu \(\overrightarrow{AB}-\overrightarrow{AD}\). Trong mặt phẳng (ABCD), tìm vectơ hiệu \(\overrightarrow{A'B'}-\overrightarrow{A'D'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}\), \(\overrightarrow{AD}\) và \(\overrightarrow{A'D'}\), \(\overrightarrow{DB}\) và \(\overrightarrow{D'B'}\).
c) Giải thích tại sao \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{A'B'}-\overrightarrow{A'D'}\).
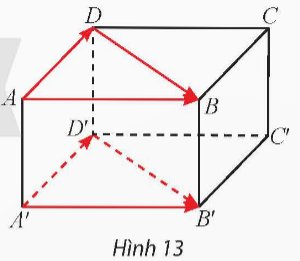
a) $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{D B} ; \overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}=\overrightarrow{D^{\prime} B^{\prime}}$
b) Vi $A A^{\prime} B^{\prime} B$ là hình bình hành, suy ra $A B / / A^{\prime} B^{\prime}$ và $A B=A^{\prime} B^{\prime}$.
Ta có hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{A^{\prime} B^{\prime}}$ cùng hướng và có độ dài bằng nhau nên $\overrightarrow{A B}=\overrightarrow{A^{\prime} B^{\prime}}$
Tương tự $\overrightarrow{A D}=\overrightarrow{A^{\prime} D^{\prime}} ; \overrightarrow{D B}=\overrightarrow{D^{\prime} B^{\prime}}$.
c) vi $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{D B} ; \overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}=\overrightarrow{D^{\prime} B^{\prime}}$ mà $\overrightarrow{D B}=\overrightarrow{D^{\prime} B^{\prime}}$ nên $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}$


