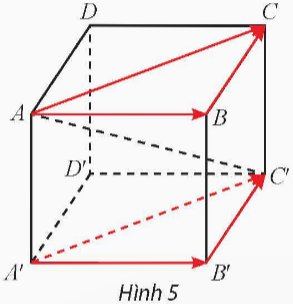
Cho hình hộp ABCD.A'B'C'D' (Hình 5).
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow{AB}+\overrightarrow{BC}\). Trong mặt phẳng (A'B'C'D'), tìm vectơ tổng \(\overrightarrow{A'B}'+\overrightarrow{B'C'}\)
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}\), \(\overrightarrow{BC}\) và \(\overrightarrow{B'C'}\), \(\overrightarrow{AC}\) và \(\overrightarrow{A'C'}\).
c) Giải thích tại sao \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{A'B'}+\overrightarrow{B'C'}\).
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {BD'} = \overrightarrow {B'D'} \)
c) \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)


