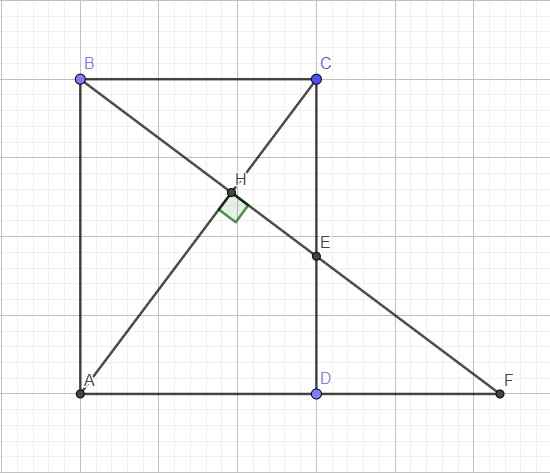
Pitago tam giác vuông ACD:
\(AC=\sqrt{AD^2+CD^2}=\sqrt{AD^2+AB^2}=20\)
Hệ thức lượng tam giác vuông ABC với đường cao BH:
\(AB^2=AH.AC\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{64}{5}\)
\(HC=AC-AH=\dfrac{36}{5}\)
b.
Hai tam giác vuông ADC và AHF có chung góc \(\widehat{HAD}\)
\(\Rightarrow\Delta_VADC\sim\Delta_VAHF\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AC}{AF}\Rightarrow AD.AF=AC.AH\) (1)
Mặt khác theo hệ thức lượng tam giác vuông ABC:
\(AB^2=AH.AC\) (2)
(1);(2) \(\Rightarrow AD.AF=AB^2\)