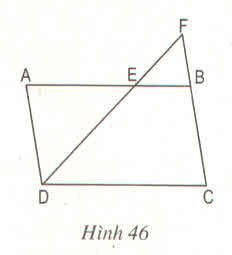
Cho hình bình hành ABCD (h.47) có độ dài các cạnh AB = 12cm, BC = 6cm. Trên cạnh AB lấy một điểm E sao cho BE = 4cm. Đường thẳng DE cắt cạnh CB kéo dài tại F.
a) Trong hình vẽ đã cho cí bao nhiêu cặp tam giác đồng dạng với nhau? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.
b) Tính độ dài các cạnh CF và BF.
c) Gọi I là giao điểm của AC và DE. Tính tỉ số IA trên IC.
d) Chứng minh rằng: FD.EA = DC.DE
e) Chứng minh rằng: DI^2 = IE.IF
Hình bạn tự vẽ nha, cảm ơn nhìu ![]()
Mà lần sau bạn đừng nhấn dáu cách nhiều quá làm mình khó xem đề ![]()
a)Ta có: BE//CD\(\Rightarrow\Delta BEF\sim\Delta CDF\)
AD//BF(AD//BC mà F\(\in\)BC)\(\Rightarrow\Delta ADE\sim\Delta BFE\)
Do đó: \(\Delta ADE\sim\Delta CDF\)
b)Xét \(\Delta CDF\), có: BE//CD
\(\Rightarrow\frac{BF}{CF}=\frac{BE}{CD}\)
\(\Leftrightarrow\frac{BF}{BE}=\frac{CF}{CD}\)(t/c tỉ lệ thức)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{BF}{BE}=\frac{CF}{CD}=\frac{CF-BF}{CD-BE}=\frac{BC}{12-4}=\frac{6}{8}=\frac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{BF}{BE}=\frac{3}{4}\Leftrightarrow BF=\frac{4.3}{4}=3\\\frac{CF}{CD}=\frac{3}{4}\Leftrightarrow CF=\frac{12.3}{4}=9\end{matrix}\right.\)
Vậy ...
c)Ta có: AE=AB-BE=12-4=8(cm)
Xét \(\Delta AEI\), có: AE//CD(E\(\in\)AB mà AB//CD)
\(\Rightarrow\frac{IA}{IC}=\frac{AE}{CD}=\frac{8}{12}=\frac{2}{3}\)
Câu d,e từ từ làm nha ![]()
Giải câu d đây:
d)Ta có: \(1-\frac{DE}{FD}=\frac{FD-DE}{FD}=\frac{EF}{FD}\)
..............\(1-\frac{EA}{DC}=\frac{DC-EA}{DC}=\frac{BE}{DC}\)(do DC=AB mà AB-EA=BE)
Trong \(\Delta CDF\), có: BE//DC (cmt)
\(\Rightarrow\frac{EF}{FD}=\frac{BE}{DC}\)(hệ quả đ/l Ta-lét)
Do đó: \(1-\frac{DE}{FD}=1-\frac{EA}{DC}\)
\(\Leftrightarrow\frac{DE}{FD}=\frac{EA}{DC}\)
\(\Leftrightarrow FD.EA=DC.DE\)
câu e để mình nghiên cứu đã ![]()
e)Cm: FC=9(cm)
Ta có:
AD//CF\(\Rightarrow\frac{DI}{IF}=\frac{AD}{FC}=\frac{6}{9}=\frac{2}{3}\)
AE//CD\(\Rightarrow\frac{IE}{DI}=\frac{AE}{DC}=\frac{8}{12}=\frac{2}{3}\)
Do đó: \(\frac{DI}{IF}=\frac{IE}{DI}\)
\(\Leftrightarrow DI^2=IE.IF\)(đpcm)