Question

Cho hình 72, trong đó ABCD là hình bình hành.

a) Chứng minh rằng AHCK là hình bình hành.

b) Gọi O là trung điểm của HK. Chứng minh rằng 3 điểm A, O, C thẳng hàng.

Answer 1

Hình đâu ạ?

Answer 2

Giải

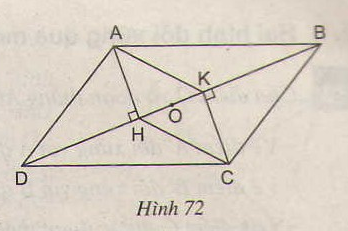
a) Ta có: AH \(\perp\)DB; CK \(\perp\)DB \(\Rightarrow\)AH//DB         (1)

Xét tam giác AHD và tam giác CKB có:

AD=BC (gt)

B=D=90\(^0\)

Góc ADH=CBK ( so le trong, AD//BC)

\(\Rightarrow\)AHD=CKB ( Cạnh huyền - góc nhọn)

\(\Rightarrow\)AH=CK (2 cạnh tương ứng)                       (2)

Từ (1) và (2) suy ra: AHCK là hình bình hành

b) Ta có: AHCK là hình bình hành nên O là trung điểm của HK theo tính chất của hình bình hành ta có O là trung điểm của AC.

\(\Rightarrow\)A, O, C thẳng hàng

 

Answer 3

a)

Xét tứ giác AHCK có : \(AH\perp BD\)

                                                 \(CK\perp BD\)

                                => AH//CK               (1)

Xét hai tam giác vuông AHD và CKB

\(+\widehat{D_1}=\widehat{B_1}\) (slt;AD//BC)

+ AD=BC( ABCD là hình bình hành)

=> AH=CK( hai cạnh tương ứng)              (2)

Từ (1) và (2) => AHCK là hình bình hành(dấu hiệu 3)

b)

Vì AHCK là hình bình hành có O là trung điểm của đường chéo HK

nên: O cũng là trung điểm của đường chéo AC.

Do đó ba điểm A,O,C thẳng hàng.

^...^  ^_^

 

 

Answer 4

Hình bình hành ABCD, ta được : AD = BC; AD // BC

Xét ΔAHD và ΔCKB, ta có :

AD = BC (cmt)

(gt)

(so le trong)

=> ΔAHD = ΔCKB (cạnh huyền – góc nhọn)

=> AH = CK

Mặt khác :

AH BD (gt)

CK BD (gt)

=> AH // CK

Xét tứ giác AHCK, ta có :

AH = CK (cmt)

AH // CK (cmt)

=> AHCK là Hình bình hành.