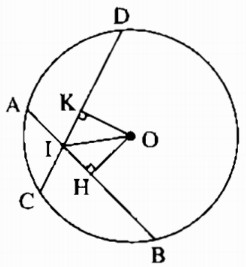
a) Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Vậy OI là tia phân giác cảu góc BID (tính chất đường phân giác)
b) Xét hai tam giác OIH và OIK, ta có:
ˆOHI=ˆOKI=90∘OHI^=OKI^=90∘
OI chung
OH = OK (chứng minh trên)
Suy ra: ∆OIH = ∆OIK (cạnh huyền, cạnh góc vuông)
Suy ra: IH = IK (1)
Lại có: HA=HB=12ABHA=HB=12AB
KC=KD=12CDKC=KD=12CD
Mà AB = CD nên HA = KC (2)
Từ (1) VÀ (2) suy ra: IA = IC
Mà A = CD nên IB = ID.








