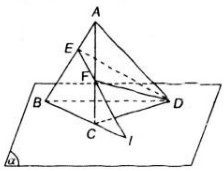
a) E, F ∈ (ABC) => EF ⊂ (ABC)
b) I ∈ EF => I ∈ ( DEF)

a) E, F ∈ (ABC) => EF ⊂ (ABC)
b) I ∈ EF => I ∈ ( DEF)

a) E, F ∈ (ABC) => EF ⊂ (ABC)
b) I ∈ EF => I ∈ ( DEF)

a) E, F ∈ (ABC) => EF ⊂ (ABC)
b) I ∈ EF => I ∈ ( DEF)
Cho tứ giác ABCD nằm trong mặt phẳng \(\left(\alpha\right)\) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng \(\left(\alpha\right)\) và M là trung điểm đoạn SC
a) Tìm giao điềm N của đường thẳng SD và mặt phẳng (MAB) ?
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy ?
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng (a , b) tại I khác O . Gọi M là điểm di động trên c và khác I . Chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên một mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng(a , b) tại điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên 1 mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng(a , b) tại điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên 1 mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mặt phẳng (a,b) tại I khác O . Gọi M là điểm di động trên c và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) cùng nằm trên một mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mp(a,b) ở điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) nằm trên một mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mp(a,b) ở điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) nằm trên một mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mp(a,b) ở điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) nằm trên một mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mp(a,b) ở điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) nằm trên một mặt phẳng cố định .