Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác cân ABC (AB = AC), O là trung điểm của cạnh đáy BC. Một điểm D di động trên cạnh AB. Trên cạnh AC lấy một điểm E sao cho CE=OB^2:BD=. Chứng minh:
a;Tam giác DBO ~Tam giác OCE
b;Tam giác DBO đồng dạng với 2 tam giác trên
c;DO pg góc BDE,IO pg góc CED
d;Khoảng cách từ O->ED không đổi khi D di đọng trên AB
Giups mk từ câu b với ạ
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.a) Chứng minh rằng : widehat{DMI}widehat{AME}b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng : \(\widehat{DMI}=\widehat{AME}\)
b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!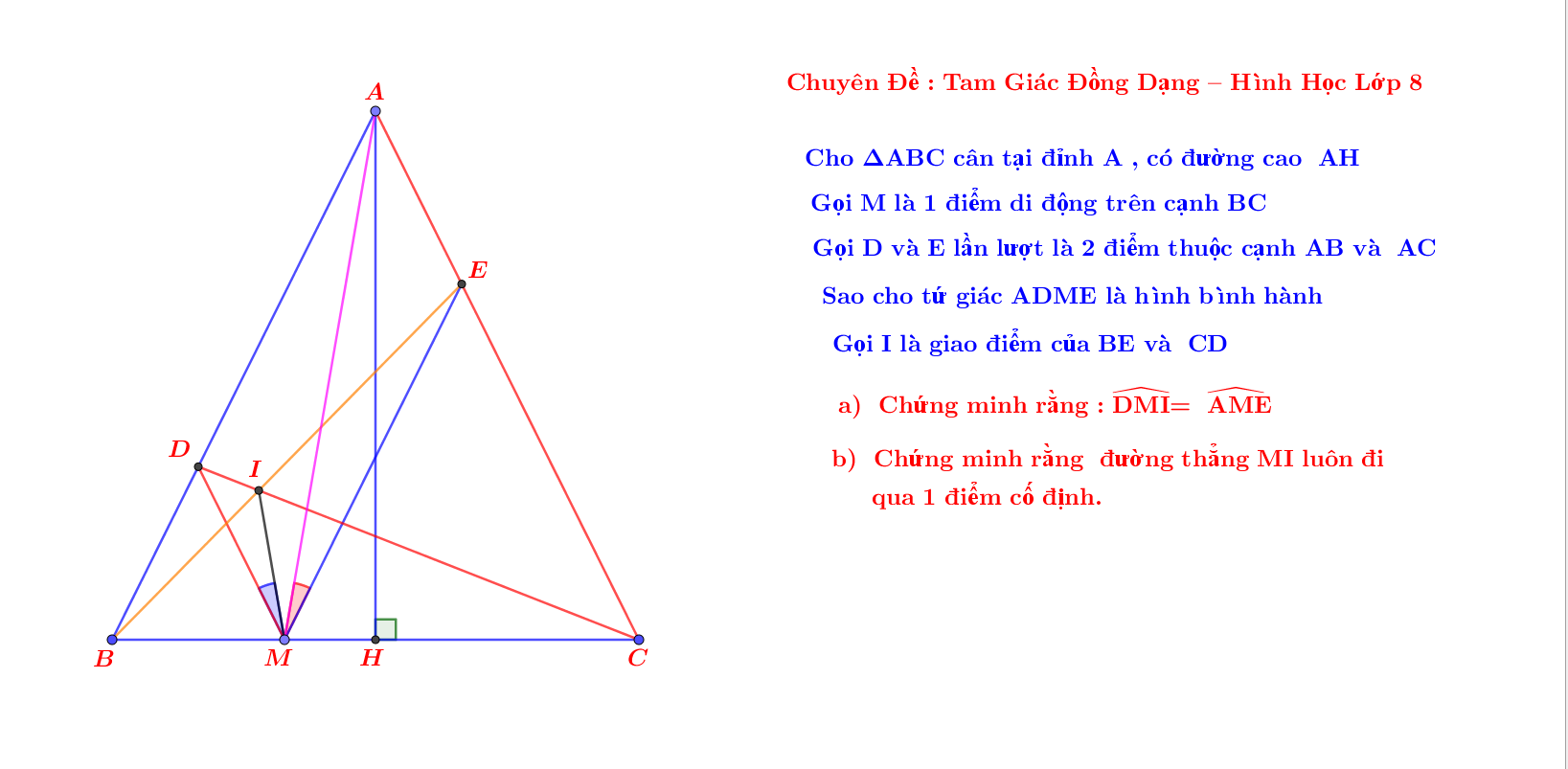
Cho ΔABC cân tại A. Gọi M là trung điểm BC. Một điểm D thay đổi trên AB. Lấy điểm E trên cạnh AC sao cho CE =\(\frac{MB^2}{BD}\) . Cmr:
a) ΔDBM ~ΔMCE
b) ΔDME ~ΔMCE
c) DM là phân giác của \(\widehat{BDE}\) , EM là phân giác \(\widehat{CED}\).
d) Khoảng cách từ điểm M đến đoạn ED không đổi khi D thay đổi trên AB.
Cho tam giác ABC có 2 đường phân giác BD và CE (D thuộc AC, E thuộc AB). Trên ED lấy điểm M bất kì, lấy L,K,H lần lượt thuộc AB,AC,BC sao cho MH ⊥ BC, ML ⊥ AB, MK ⊥ AC. chứng minh MH = ML + MK
Cho tam giác ABC cân tại A có BC = 2a, M là trung điểm của BC. Lấy các điểm D, E theo thứ tự thuộc các cạch AB, AC sao cho \(\widehat{DME}\) = \(\widehat{B}\)
a) Chứng minh BC. CE không đổi.
b) Chứng minh DM là tia phân giác của góc BDE.
c) Tính chu vi tam giác AED nếu tam giác ABC đều.
Cho tam giác ABC, M là trung điểm của BC. Trên cạnh AB lấy hai điểm D và E sao cho AD = DE = EB, I = AM Ç CD. Chứng minh rằng: a) ME // CD
b) I là trung điểm của AM
c) CI = 3 DI
cho góc nhọn xAy. Trên cạnh Ax lấy 2 điểm B và C sao cho AB=4cm; AC=6cm. Trên cạnh Ay lấy 2 điểm D và E sao cho AD=2cm; AE=12cm. Tia phân giác của góc xAy cắt BD tại I và cắt CE tại k.
a. so sánh AD/AB và AE/AC
b. so sánh góc ACE và góc ADB
c. cm: AI.KE=AK.IB
d. cho EC =10cm. Tính BD,DI
e. cm; KE.KC=9IB.ID
Cho hình vuông ABCD có AB = a, hai đường chéo cắt nhau tại O. Trên hai cạnh AB, BC lần lượt lấy hai điểm E và G sao cho AE= BG. Gọi H là giao điểm của tia AG và tia DC, I là giao điểm của tia OG và đoạn thẳng BH.
1) Chứng minh rằng: AOGE là tam giác vuông cân.
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.










