Question

Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.

Một phân tử metan CH₄ được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.

Góc liên kết là góc tạo bởi liên kết H – C – H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Chứng minh rằng góc liên kết này gần bằng 109,5°.

Answer 1

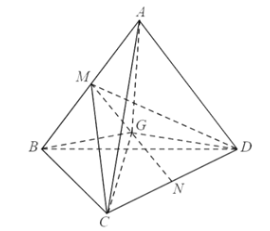
Gọi G là trọng tâm của tứ diện đều ABCD.
Đặt $\vec{a}=\overrightarrow{G A}, \vec{b}=\overrightarrow{G B}, \vec{c}=\overrightarrow{G C}, \vec{d}=\overrightarrow{G D}$
Ta có $|\vec{a}|=|\vec{b}|=|\vec{c}|=|\vec{d}|$ và $\vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}=\vec{a} \cdot \vec{d}=\vec{b} \cdot \vec{c}=\vec{b} \cdot \vec{d}=\vec{c} \cdot \vec{d}$
Ta có $\vec{a}+\vec{b}+\vec{c}+\vec{d}=\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G D}=\overrightarrow{0}$
$$
\begin{aligned}
& \Rightarrow(\vec{a}+\vec{b}+\vec{c}+\vec{d})^2=0 \\
& \Rightarrow \overrightarrow{\mathrm{a}}^2+\overrightarrow{\mathrm{b}}^2+\overrightarrow{\mathrm{c}}^2+\overrightarrow{\mathrm{d}}^2+2 \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{~b}}+2 \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{c}}+2 \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{~d}}+2 \overrightarrow{\mathrm{~b}} \cdot \overrightarrow{\mathrm{c}}+2 \overrightarrow{\mathrm{~b}} \cdot \overrightarrow{\mathrm{~d}}+2 \overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{~d}}=0 \\
& \Rightarrow 4 \vec{a}^2+12 \cdot \vec{a} \cdot \vec{b}=0 \\
& \Rightarrow \frac{\vec{a} \cdot \vec{b}}{\vec{a}^2}=-\frac{1}{3} \\
& \Rightarrow \cos (\vec{a}, \vec{b})=-\frac{1}{3} \\
& \Rightarrow(\vec{a}, \vec{b}) \approx 109,5^{\circ}
\end{aligned}
$$

Vậy góc liên kết gần bằng $109,5^{\circ}$.