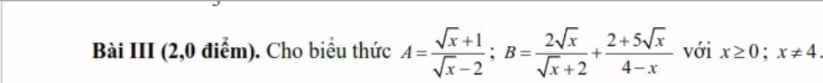Question

Cho A=\(\frac{3}{x−12\sqrt{x}+40}\)

Tìm giá trị lớn nhất của A

Giá trị đó đạt được khi x bằng bao nhiêu?

Answer 1

đkxđ: \(x\ge0\)

A=\(\frac{3}{x-12\sqrt{x}+40}=\frac{3}{\left(\sqrt{x}\right)^2-2.\sqrt{x}.6+6^2+4}\) \(=\frac{3}{\left(\sqrt{x}-6\right)^2+4}\)

vì \(\left(\sqrt{x}-6\right)^2\ge0\Rightarrow\left(\sqrt{x}-6\right)^2+4\ge4\)

\(\Leftrightarrow\frac{3}{\left(\sqrt[]{x}-6\right)^2+4}\le\frac{3}{4}\)

\(hayA\le\frac{3}{4}\) Dấu = xảy ra khi: \(\left(\sqrt{x}-6\right)^2=0\Rightarrow\sqrt{x}=6\Leftrightarrow x=36\)(tm)

vậy max A bằng 3/4 tại x=36

Answer 2

Mọi người làm chi tiết hộ ạ