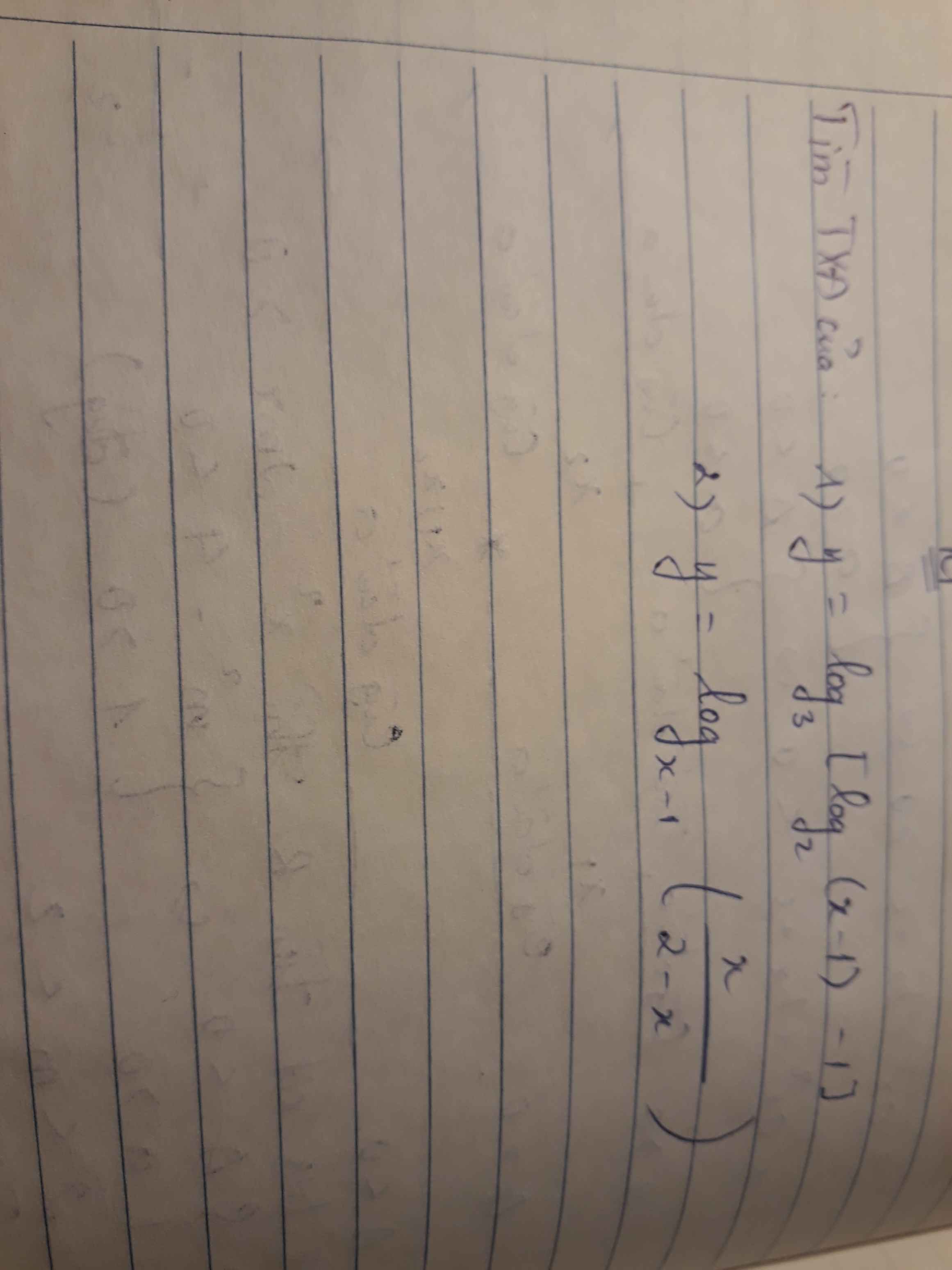câu này làm thế nào ạ
Đầu tiên ta chứng minh bổ đề: Với \(x,y\ge2\) thì
\(x+y\le xy\)
\(\Leftrightarrow2xy-2x-2y\ge0\)
\(\Leftrightarrow x\left(y-2\right)+y\left(x-2\right)\ge0\)(đúng)
Ta cần chứng minh:
\(log_{a+b}c^2+log_{b+c}a^2+log_{c+a}b^2\ge3\)
\(\Leftrightarrow log_{a+b}c+log_{b+c}a+log_{c+a}b\ge\dfrac{3}{2}\)
Ta có:
\(log_{a+b}c+log_{b+c}a+log_{c+a}b\)
\(=\dfrac{lna}{ln\left(b+c\right)}+\dfrac{lnb}{ln\left(c+a\right)}+\dfrac{lnc}{ln\left(a+b\right)}\)
\(\ge\dfrac{lna}{ln\left(bc\right)}+\dfrac{lnb}{ln\left(ca\right)}+\dfrac{lnc}{ln\left(ab\right)}\)
\(=\dfrac{lna}{lnb+lnc}+\dfrac{lnb}{lnc+lna}+\dfrac{lnc}{lna+lnb}\)
Đặt \(\left\{{}\begin{matrix}lna=x\\lnb=y\\lnc=z\end{matrix}\right.\) thì bài toán cần chứng minh trở thành
\(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\)
Đây là bất đẳng thức Nesbit việc chứng minh quá đơn giản nên mình nhường lại cho bạn làm nhé.
