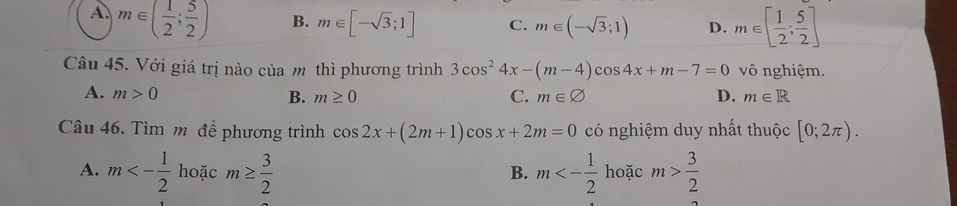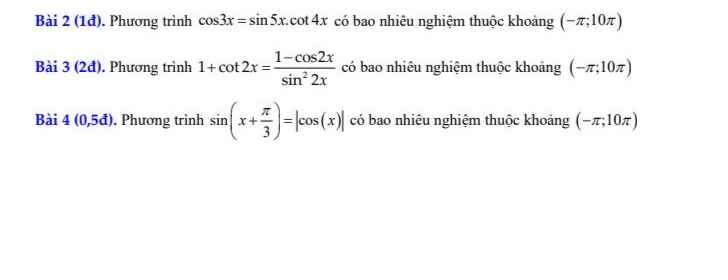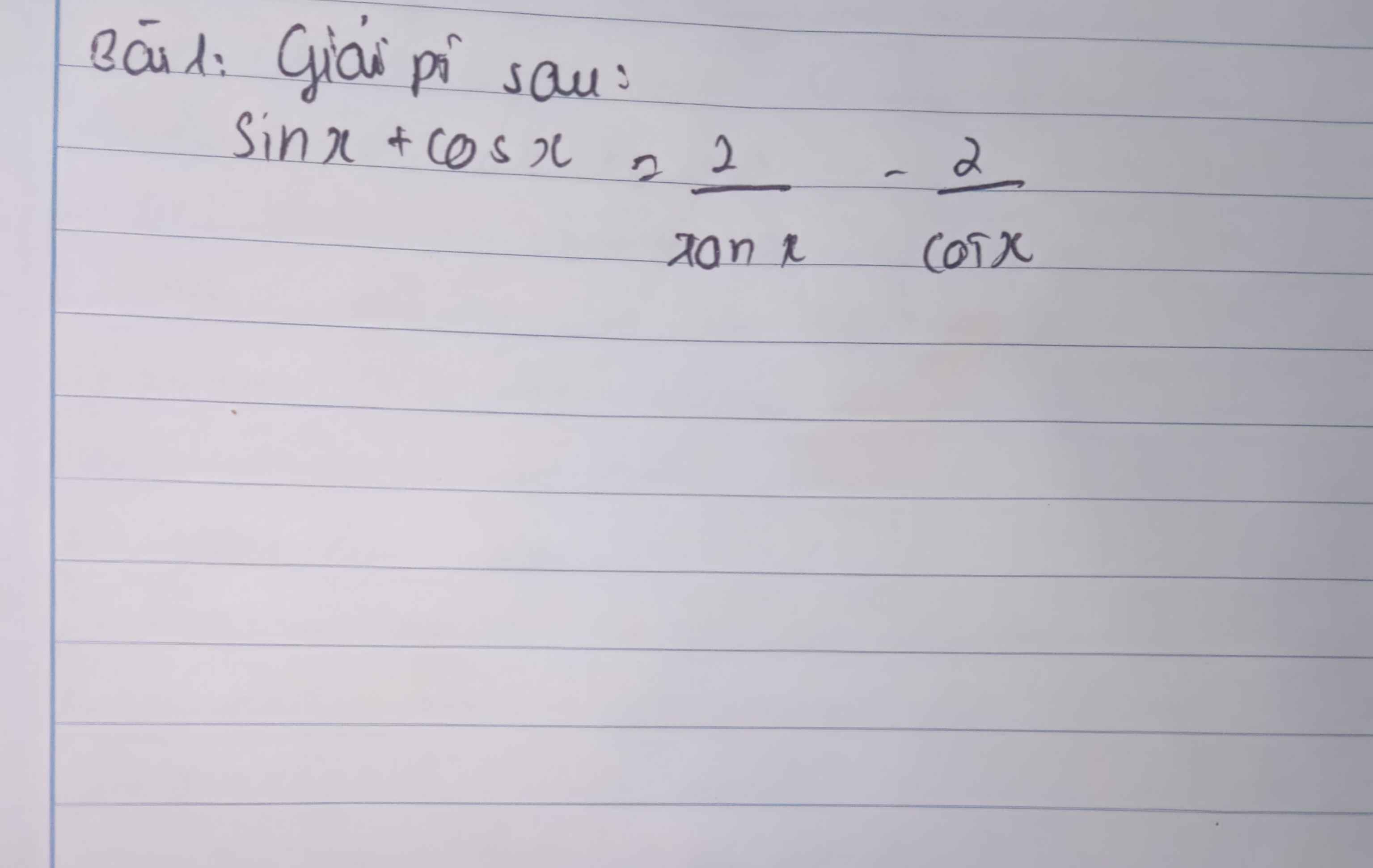Lời giải:
Đặt $\cos 4x=t, t\in [-1;1]$ thì pt trở thành:
$3t^2-(m-4)t+m-7=0$
$\Leftrightarrow 3t^2-mt+4t+m-7=0$
$\Leftrightarrow (3t^2+4t-7)-(mt-m)=0$
$\Leftrightarrow (t-1)(3t+7)-m(t-1)=0$
$\Leftrightarrow (t-1)(3t+7-m)=0$
Ta thấy pt luôn có nghiệm $t=1$ (thỏa mãn) nên không tồn tại $m$ để pt vô nghiệm.
Đáp án C>
Đúng 0
Bình luận (0)