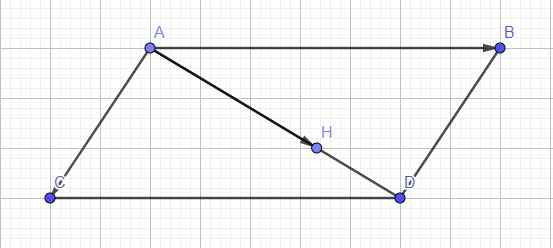
Dựng hình bình hành ABDC \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
Ta có:
\(\overrightarrow{HA}+2\overrightarrow{HB}=\overrightarrow{CB}\Leftrightarrow\overrightarrow{HA}+2\overrightarrow{HA}+2\overrightarrow{AB}=\overrightarrow{CB}\)
\(\Leftrightarrow2\overrightarrow{AB}-\overrightarrow{CB}=-3\overrightarrow{HA}\)
\(\Leftrightarrow3\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\Leftrightarrow3\overrightarrow{AH}=2\overrightarrow{AD}\)
\(\Leftrightarrow\overrightarrow{AH}=\dfrac{2}{3}\overrightarrow{AD}\)
Vậy H là điểm nằm trên đoạn thẳng AD sao cho \(\overrightarrow{AH}=\dfrac{2}{3}\overrightarrow{AD}\)