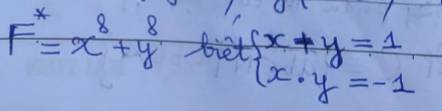6.
a, ĐK: \(x\ne2;x\ne3\)
\(P=\dfrac{2x-9}{x^2-5x+6}-\dfrac{x+3}{x-2}-\dfrac{2x+1}{3-x}\)
\(=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{x^2-9}{\left(x-2\right)\left(x-3\right)}+\dfrac{2x^2-3x-2}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9-x^2+9+2x^2-3x-2}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2-x-2}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b, \(P=\dfrac{x+1}{x-3}=-\dfrac{1}{2}\Leftrightarrow2x+2=-x+3\Leftrightarrow x=\dfrac{1}{3}\)
\(P< 1\Leftrightarrow\dfrac{x+1}{x-3}< 1\Leftrightarrow\dfrac{4}{x-3}< 0\Leftrightarrow x-3< 0\Leftrightarrow x< 3\)
a/ \(=\dfrac{2x-9-\left(x+3\right)\left(x-3\right)+\left(2x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\) ( x khác 2 ; x khác 3)
\(=\dfrac{2x-9-x^2+9+2x^2+x-4x-2}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2-x-2}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b/ \(P=\dfrac{1}{2}\Leftrightarrow\dfrac{x+1}{x-3}=\dfrac{1}{2}\)(x khác 2 ; x khác 3)
\(\Leftrightarrow x-3=2x+2\)
\(\Leftrightarrow x=-5\)
\(P< 1\Leftrightarrow\dfrac{x+1}{x-3}-1< 0\)
\(\Leftrightarrow\dfrac{4}{x-3}< 0\)
\(\Leftrightarrow x-3>0\Leftrightarrow x>3\) (tmđk)
c/ \(x^2-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(loại\right)\\x=-2\end{matrix}\right.\)
Thay x = -2 vào P ta có
\(P=\dfrac{-2+1}{-2-3}=-\dfrac{1}{-5}=\dfrac{1}{5}\)
d/ \(P=\dfrac{x+1}{x-3}\in Z^+\)
\(\Leftrightarrow1+\dfrac{4}{x-3}\) nguyên dương
\(\Leftrightarrow\dfrac{4}{x-3}\) nguyên dương
\(\Leftrightarrow x-3\in\left\{1;4\right\}\)
\(\Leftrightarrow x\in\left\{4;7\right\}\)
KHĐK x khác 2 ; x khác 3 ta có
x ∈ {4;7}
c, \(x^2-4=0\Leftrightarrow\left[{}\begin{matrix}x=2\left(l\right)\\x=-2\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{x+1}{x-3}=\dfrac{-2+1}{-2-3}=\dfrac{1}{5}\)
d, \(P=\dfrac{x+1}{x-3}=\dfrac{x-3+4}{x-3}=1+\dfrac{4}{x-3}\in N^{\text{*}}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3\in U_4=\left\{\pm1;\pm2;\pm4\right\}\\\dfrac{x+1}{x-3}>0\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{4;5;7\right\}\)








 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)

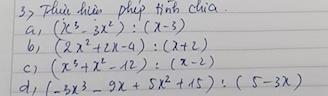


 Giúp em vs ạ
Giúp em vs ạ
 bài 7 . 8 làm giúp mil vs ạ mik đg vội
bài 7 . 8 làm giúp mil vs ạ mik đg vội