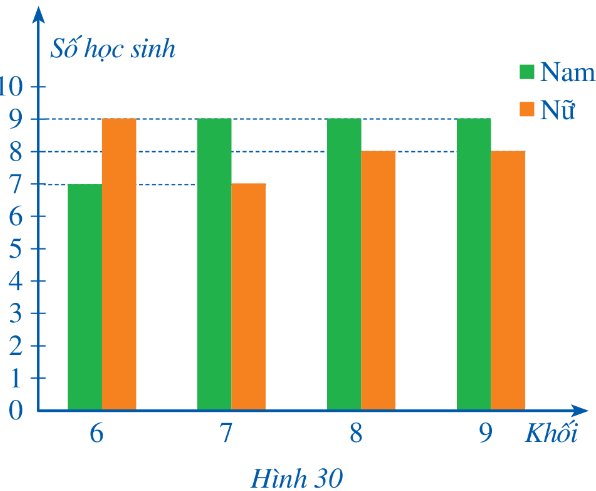
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia thi giải thi đấu thể thao của một trường THCS.
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó.
Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”.
B: “Học sinh được chọn thuộc khối 6”.
C: “Học sinh được chọn là nữ và không thuộc khối 9”.
Tổng số học sinh toàn trường tham gia giải đấu là:
7 + 9 + 9 + 7 + 9 + 8 + 9 + 8 = 66 (học sinh).
Xét phép thử: “Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó”.
Ta thấy, các kết quả có thể xảy ra của phép thử trên là đồng khả năng.
Tổng số học sinh nam toàn trường tham gia giải đấu là:
7 + 9 + 9 + 9 = 34 (học sinh nam).
Tổng số học sinh thuộc khối 6 tham gia giải đấu là:
7 + 9 = 16 (học sinh).
Tổng số học sinh nữ không thuộc khối 9, tức là thuộc khối 6, 7, 8 tham gia giải đấu là:
9 + 7 + 8 = 24 (học sinh).
Xác suất của biến cố A là: \(P\left(A\right)=\dfrac{34}{66}=\dfrac{17}{33}.\)
Xác suất của biến cố B là: \(P\left(B\right)=\dfrac{16}{66}=\dfrac{8}{33}.\)
Xác suất của biến cố C là: \(P\left(C\right)=\dfrac{24}{66}=\dfrac{4}{11}\).
Tổng số học sinh toàn trường tham gia giải đấu là:
7 + 9 + 9 + 7 + 9 + 8 + 9 + 8 = 66 (học sinh).
Xét phép thử: “Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó”.
Ta thấy, các kết quả có thể xảy ra của phép thử trên là đồng khả năng.
Tổng số học sinh nam toàn trường tham gia giải đấu là:
7 + 9 + 9 + 9 = 34 (học sinh nam).
Tổng số học sinh thuộc khối 6 tham gia giải đấu là:
7 + 9 = 16 (học sinh).
Tổng số học sinh nữ không thuộc khối 9, tức là thuộc khối 6, 7, 8 tham gia giải đấu là:
9 + 7 + 8 = 24 (học sinh).
Xác suất của biến cố A là: \(P\left(A\right)=\dfrac{34}{66}=\dfrac{17}{33}.\)
Xác suất của biến cố B là: \(P\left(B\right)=\dfrac{16}{66}=\dfrac{8}{33}.\)
Xác suất của biến cố C là: \(P\left(C\right)=\dfrac{24}{66}=\dfrac{4}{11}\).


