12
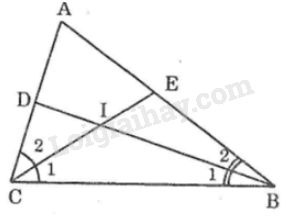
a) ∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o
b) Ta có:
+ Trong ΔBIC có ∠BIC = 180o - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180o - 1/2.(180 - ∠A) = 90o + 1/2.∠A
∠A = 80o ⇒ ∠BIC = 90 + 1/2.80o = 130o.
∠A = mo ⇒ ∠BIC = 90o + 1/2.mo.
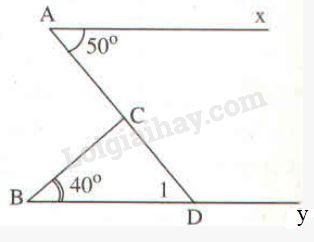
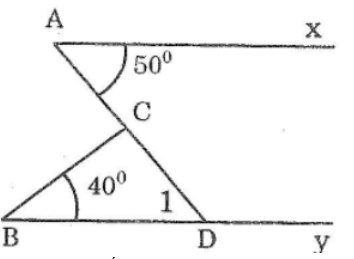
13
Kéo dài AC cắt By tại D
Vì By // Ax suy ra ∠(D1) = ∠A (hai góc so le trong)
Mà ∠A = 50o(gt) nên ∠∠(D1) = 50o
TrongΔBCD ta có ∠(ACB) là góc ngoài tại đỉnh C
⇒∠(ACB) = ∠B + ∠(D1) (tính chất góc ngoài của tam giác)
⇒∠(ACB) = 40o + 50o = 90o
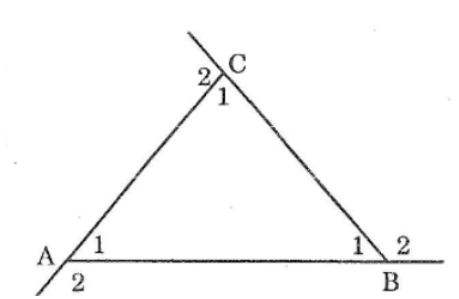
14
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai goác kề bù)
∠(B1 ) +∠(B2 ) =180o(hai goác kề bù)
∠(C1 ) +∠(C2 )=180o(hai goác kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) =180.3=540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
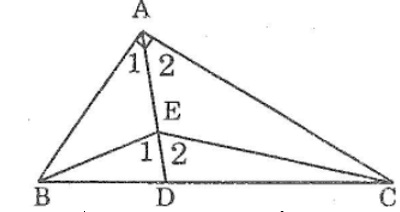
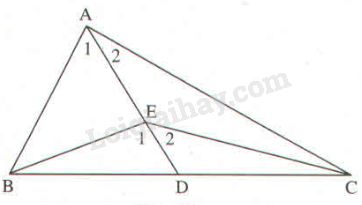
15Trong ∆ABE ta có ∠E1 là góc ngoài tại đỉnh E
Suy ra: ∠E1 >∠A1 (tính chất góc ngoài tam giác)(1)
Trong ∆AEC ta có ∠E2 là góc ngoài tại đỉnh E
Suy ra: ∠E2 > ∠A2 (tính chất góc ngoài tam giác)(2)
Cộng từng vế (1) và (2) ta có:
∠E2 +∠E2 >∠A2 +∠A1
Hay (BEC) > (BAC) =90o
Vậy (BEC) là góc tù.
Nguồn: loigiaihay.com
Bài 12:
Bài 13:
Bài 14:
Bài 15:
Chúc bạn học tốt!
giúp mình nha!!!! mai mình học rồi cảm ơn các bạn nhiều!!!!
