Question

Bài 8: Vẽ hai góc có chung đỉnh và có cùng số đo là 70°, nhưng không đối đỉnh.

Bài 9: Vẽ góc vuông xAy. Vẽ góc x'Ay' đối đỉnh với góc xAy. Hãy viết tên hai góc vuông không đối đỉnh.

Answer 1

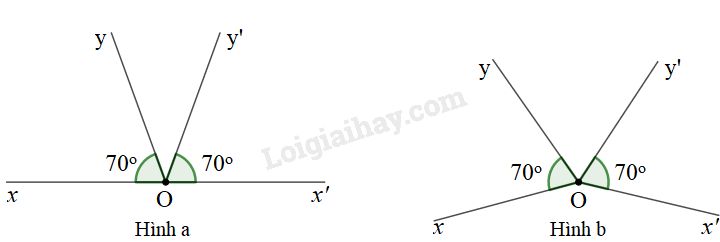
Bài 8 :

Có thể vẽ như sau:

a) Vẽ đường thẳng $x{x}^{\prime }$. Trên $x^{\prime }x$ lấy điểm $O.$

Vẽ $\widehat{xOy}={70}^{\circ }$ và $\widehat{x^{\prime }O{y}^{\prime }}={70}^{\circ }$ (hình a).

b) Vẽ $\widehat{xOy}={70}^{\circ }$.

Từ $O$ vẽ tia $O{x}^{\prime }$ bất kì (không phải là tia đối của $Ox,Oy$).

Vẽ $\widehat{x^{\prime }O{y}^{\prime }}={70}^{\circ }$ (hình b).

Bài 9

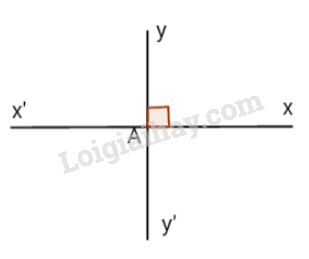
- Dựng $A{x}^{\prime }$ là tia đối của tia $Ax,A{y}^{\prime }$ là tia đối của tia $Ay.$ Khi đó ta có $\widehat{x^{\prime }A{y}^{\prime }}$đối đỉnh với góc $\widehat{xAy}.$

- Hai góc vuông không đối đỉnh là:

$\widehat{xAy}$ và $\widehat{x^{\prime }Ay}$;

$\widehat{xAy}$ và $\widehat{xA{y}^{\prime }}$;

$\widehat{xA{y}^{\prime }}$ và $\widehat{x^{\prime }A{y}^{\prime }}$;

$\widehat{x^{\prime }Ay}$ và $\widehat{x^{\prime }A{y}^{\prime }}.$

Answer 2

Bài 8:

Bài 9:

Ta có: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là 2 góc đối đỉnh.

=> \(\widehat{xAy}=\widehat{x'Ay'}\)

Mà \(\widehat{xAy}=90^0\left(gt\right)\)

=> \(\widehat{x'Ay'}=90^0.\)

=> \(xx'\) và \(yy'\) cắt nhau tại A.

Lại có: \(\widehat{yAx'}=\widehat{xAy'}\) (vì 2 góc đối đỉnh)

Mà \(\widehat{xAy}+\widehat{yAx'}=\widehat{xAx'}\)

=> \(90^0+\widehat{yAx'}=180^0\)

=> \(\widehat{yAx'}=180^0-90^0\)

=> \(\widehat{yAx'}=90^0.\)

=> \(\widehat{xAy'}=90^0.\)

Các cặp góc vuông không đối đỉnh là:

+ \(\widehat{xAy}\) và \(\widehat{yAx'}.\)

+ \(\widehat{yAx'}\) và \(\widehat{x'Ay'}.\)

+ \(\widehat{x'Ay'}\) và \(\widehat{y'Ax}.\)

+ \(\widehat{y'Ax}\) và \(\widehat{xAy}.\)

Chúc bạn học tốt!

Answer 3

vũ minh tuấn vẽ hình sai bài 9

Answer 4

vẫn có cặp góc đối đỉnh