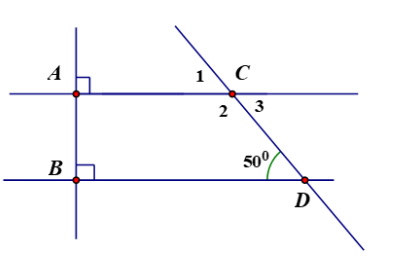
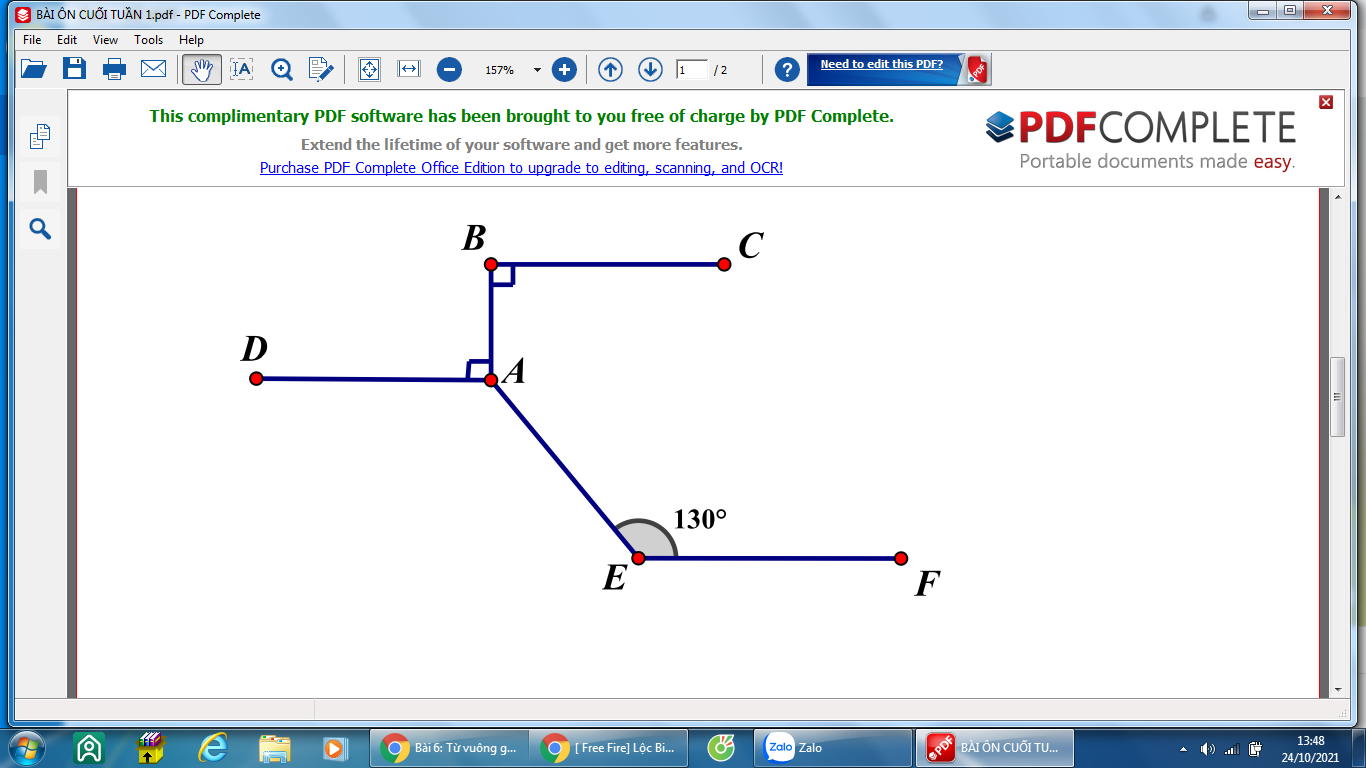
a) a // b
\(\Rightarrow\) \(\widehat{ACD}\) + \(\widehat{CDB}\) = 180\(^O\) ( hai góc trong cùng phía )
\(\Rightarrow\) \(\widehat{ACD}\) = 180\(^O\) - \(\widehat{CDB}\) = 180\(^O\) - 65\(^O\) = 115\(^O\)
\(\Rightarrow\) \(\widehat{ACD}\) = \(\widehat{C_1}\) ( hai góc đối đỉnh )
mà \(\widehat{ACD}\) = 115\(^O\) \(\Rightarrow\) \(\widehat{C_1}\) = 115\(^O\)
\(\widehat{CDB}\) = \(\widehat{C_2}\) ( hai góc so le trong )
mà \(\widehat{CDB}\) = 65\(^O\) \(\Rightarrow\) \(\widehat{C_2}\) = 65\(^O\)
\(\widehat{C_1}\) = \(\widehat{D_1}\) ( hai góc đồng vị )
mà \(\widehat{C_1}\) = 115\(^O\) \(\Rightarrow\) \(\widehat{D_1}\) = 115\(^O\)
Vậy \(\widehat{ACD}\) = 115\(^O\)
\(\widehat{C_1}\) = 115\(^O\)
\(\widehat{C_2}\) = 65\(^O\)
\(\widehat{D_1}\) = 115\(^O\)