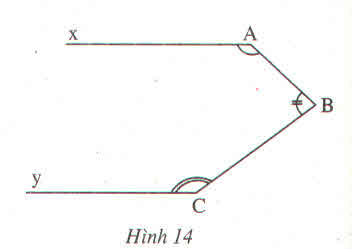
Kẻ Bz // Ax ( Bz nằm khác phía với Ax)
=> \(\widehat{A}=\widehat{ABz}\left(soletrong\right)\)
Vì Bz // Ax
mà Ax // Cy
=> Bz // Cy
=> \(\widehat{C}=\widehat{zBC}\left(soletrong\right)\)
Ta có: \(\widehat{ABz}+\widehat{zBC}=\widehat{ABC}\)
hay \(\widehat{A}+\widehat{C}=\widehat{ABC}\) (đpcm)
Qua B kẻ tia Bz // Ax
Suy ra: góc BAx = góc ABz ( hai góc sole trong)(1)
Ta có: Ax//Bz
Ax//Cy
===> Cy//Bz
===> góc CBz = góc BCy(2 góc so le trong)(2)
Vì tia Bz nằm giữa 2 tia AB và BC nên: góc ABz + góc CBz = góc ABC(3)
Từ (1)(2)(3) suy ra : góc A + góc C = góc ABC