Question

?

Answer 1

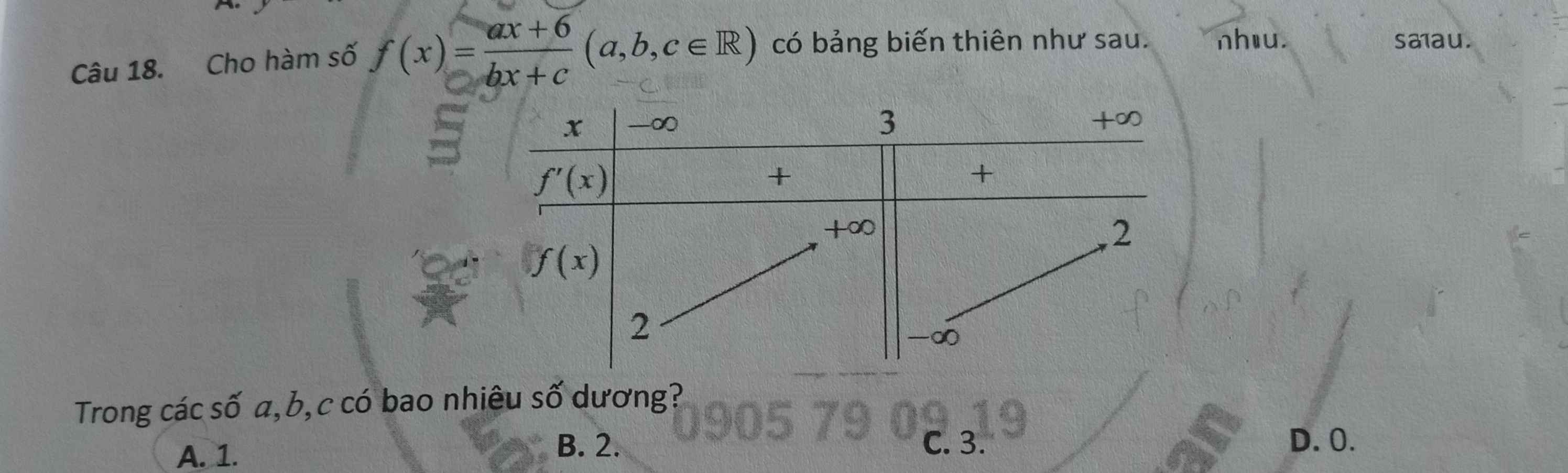
\(x=-\dfrac{c}{b}\) là tiệm cận đứng \(\Rightarrow-\dfrac{c}{b}=3\Rightarrow c=-3b\) 

\(y=2\) là tiệm cận ngang \(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+6}{bx+c}=\dfrac{a}{b}=2\Rightarrow a=2b\)

Hàm đồng biến trên các khoảng xác định \(\Rightarrow ac-6b>0\)

\(\Rightarrow2b.\left(-3b\right)-6b>0\Rightarrow b\left(b+1\right)< 0\)

\(\Rightarrow-1< b< 0\)

\(\Rightarrow a=2b< 0;c=-3b>0\)

Vậy có đúng 1 số dương là c (A là đáp án đúng)