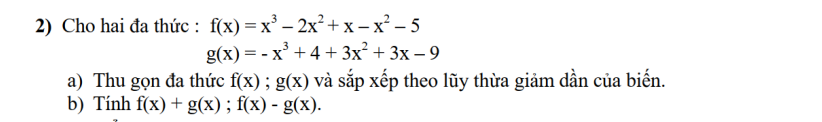a) f(x) = x3 - 2x2 + x - x2 - 5
= x3 + ( -2x2 - x2 ) + x - 5
= x3 - 3x2 + x - 5
g(x) = -x3 + 4 + 3x2 + 3x - 9
= -x3 + 3x2 + 3x + ( 4 - 9)
= -x3 + 3x2 + 3x - 5
b) f(x) + g (x)= x3 - 3x2 + x - 5 - x3 + 3x2 + 3x - 5
= ( x3 - x3 ) + ( -3x2 + 3x2 ) + ( x + 3x ) + ( -5 - 5 )
= 4x - 10
f(x) - g(x) = x3 - 3x2 + x - 5 - ( -x3 + 3x2 + 3x - 5)
= x3 - 3x2 + x - 5 + x3 - 3x2 - 3x + 5
= ( x3 + x3 ) + ( -3x2 - 3x2 ) + ( x - 3x ) + ( -5 + 5)
= 2x3 - 6x2 - 2x