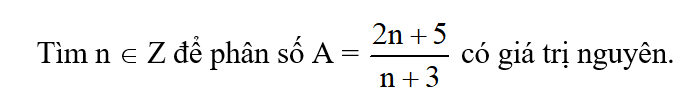Question

Answer 1

\(A=\dfrac{2n+5}{n+3}\)

\(A=\dfrac{2n+5}{n+3}=\dfrac{2\left(n+3\right)-1}{n+3}=\dfrac{2-1}{n+3}\)

A có giá trị là số nguyên thì 

\(1⋮n+3\) \(\Rightarrow n+3\inƯ\left(1\right)=\) {\(-1;1\)} 

\(n+3=1\Rightarrow n=-2\)

\(n+3=-1\Rightarrow n=-4\)

Vậy \(n\in\left(-2;-4\right)\)

 

Answer 2

\(A=\dfrac{2\left(n+3\right)}{n+3}-\dfrac{1}{n+3}\)

\(=2-\dfrac{1}{n+3}\)

Để A nguyên \(\Rightarrow\dfrac{1}{n+3}\) nguyên

\(\Rightarrow\left(n+3\right)\inƯ\left(1\right)=\left\{\pm1\right\}\)

Còn lại tự xét nha