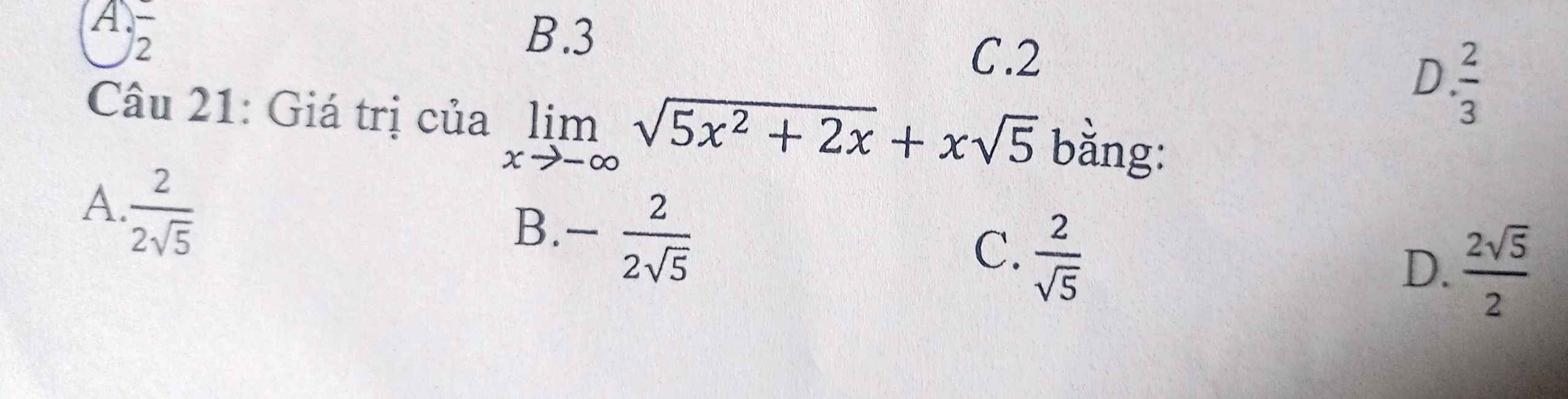Question

Answer 1

lỗi r bn

Answer 2

lx

Answer 3

\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{5x^2+2x}+x\sqrt{5}\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(\sqrt{5x^2+2x}+x\sqrt{5}\right)\left(\sqrt{5x^2+2x}-x\sqrt{5}\right)}{\sqrt{5x^2+2x}-x\sqrt{5}}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{2x}{\sqrt{5x^2+2x}-x\sqrt{5}}=\lim\limits_{x\rightarrow-\infty}\dfrac{2x}{x\left(-\sqrt{5+\dfrac{2}{x}}-\sqrt{5}\right)}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{2}{-\sqrt{5+\dfrac{2}{x}}-\sqrt{5}}=-\dfrac{2}{2\sqrt{5}}\)