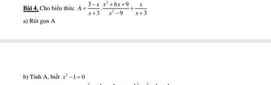\(Đkxđ:x\ne\pm3\\ =\dfrac{3-x}{x+3}.\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\\ \Leftrightarrow-\dfrac{x-3}{x-3}+\dfrac{x}{x+3}=-1+\dfrac{x}{x+3}\\ \Leftrightarrow\dfrac{x}{x+3}-1=\dfrac{x-x-3}{x+3}=\dfrac{-3}{x+3}\\ \Rightarrow A=\dfrac{-3}{x+3}\)
\(x^2-1=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ Thay.x=1\\ =\dfrac{-3}{1+3}=\dfrac{-3}{4}\\ Thay.x=-1\\ =\dfrac{-3}{-1+3}=\dfrac{-3}{2}\)
a, \(A=\dfrac{-\left(x-3\right)\left(x+3\right)^2}{\left(x+3\right)^2\left(x-3\right)}+\dfrac{x}{x+3}=-1+\dfrac{x}{x+3}=\dfrac{-x-3+x}{x+3}=-\dfrac{3}{x+3}\)
b, Ta có : \(x^2-1=0\Leftrightarrow x=1;x=-1\)(tm)
Với x = 1 => A = -3/4
Với x = -1 => A = -3/2
Lời giải:
a. ĐKXĐ: $x\neq \pm 3$
\(A=\frac{3-x}{x+3}.\frac{(x+3)^2}{(x-3)(x+3)}+\frac{x}{x+3}=-1+\frac{x}{x+3}=\frac{-3}{x+3}\)
b. $x^2-1=0\Leftrightarrow (x-1)(x+1)=0\Leftrightarrow x-1=0$ hoặc $x+1=0$
$\Leftrightarrow x=1$ hoặc $x=-1$
Thay vô biểu thức $A$:
Nếu $x=1$ thì $A=\frac{-3}{x+3}=\frac{-3}{1+3}=\frac{-3}{4}$
Nếu $x=-1$ thì $A=\frac{-3}{x+3}=\frac{-3}{-1+3}=\frac{-3}{2}$