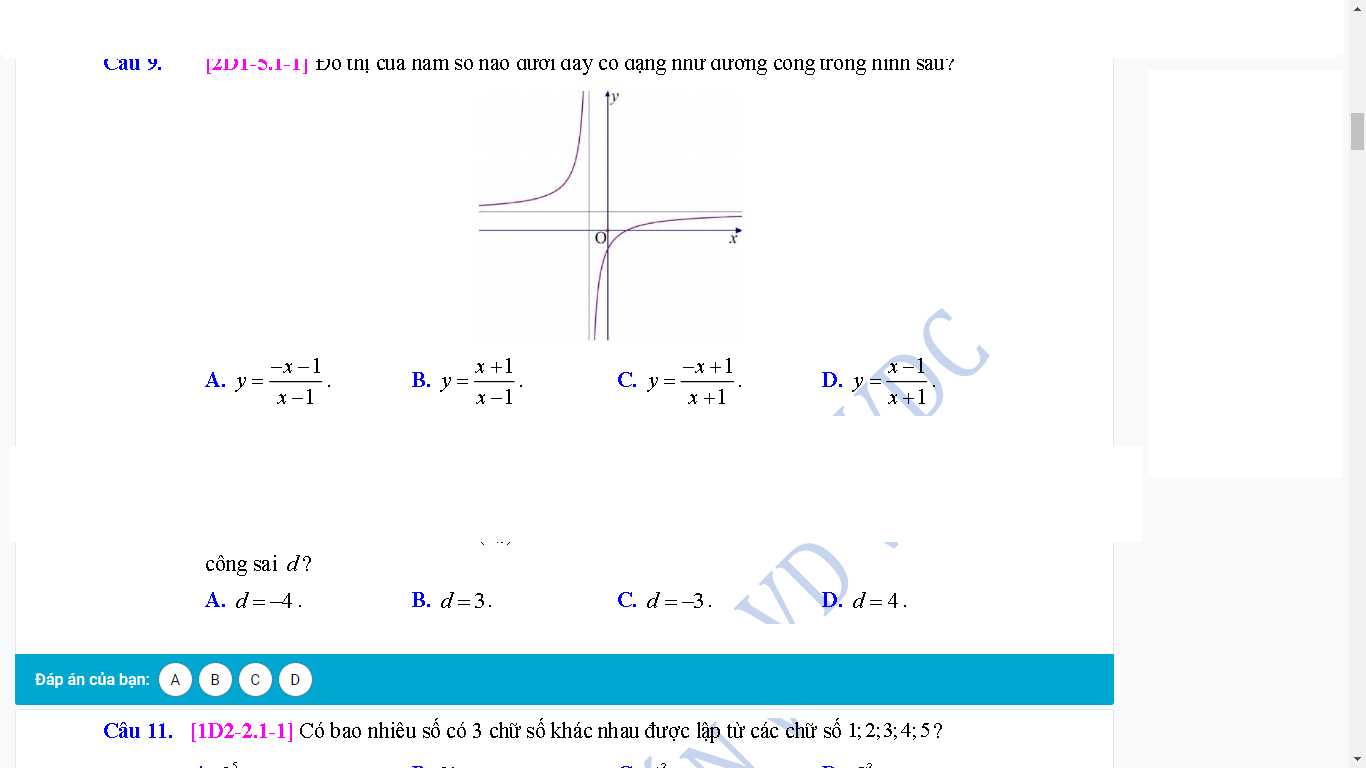
TXĐ: D=R
\(y'=-x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=2\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow\pm\infty}y=-\infty\)
BBT:
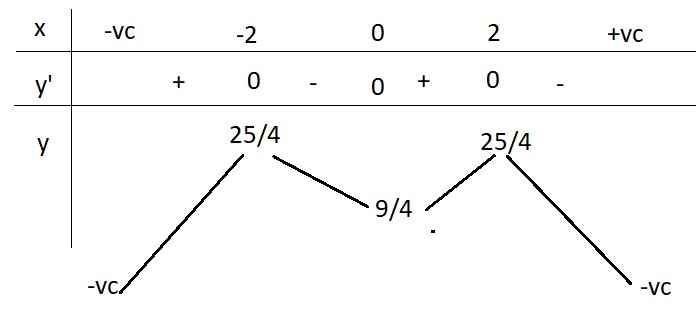
Hàm đồng biến trên các khoảng \(\left(-\infty;-2\right)\) và \(\left(0;2\right)\)
Hàm nghịch biến trên các khoảng \(\left(-2;0\right)\) và \(\left(2;+\infty\right)\)
Đồ thị bạn tự vẽ
b.
\(x^4-8x^2+m=0\)
\(\Leftrightarrow-\dfrac{1}{4}x^4+2x^2=\dfrac{m}{4}\)
\(\Leftrightarrow-\dfrac{1}{4}x^4+2x^2+\dfrac{9}{4}=\dfrac{m+9}{4}\)
Từ đồ thị ta thấy \(y=\dfrac{m+9}{4}\) cắt \(y=f\left(x\right)\) tại 4 điểm phân biệt khi và chỉ khi:
\(\dfrac{9}{4}< \dfrac{m+9}{4}< \dfrac{25}{4}\)
\(\Rightarrow0< m< 16\)
c.
Phương trình hoành độ giao điểm:
\(-\dfrac{1}{4}x^4+2x^2+\dfrac{9}{4}=0\Rightarrow\left[{}\begin{matrix}x^2=9\\x^2=-1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
Tại \(x=3\Rightarrow y'\left(3\right)=-15\)
Phương trình tiếp tuyến: \(y=-15\left(x-3\right)\Leftrightarrow y=-15x+45\)
Tại \(x=-3\Rightarrow y'\left(-3\right)=15\)
Phương trình tiếp tuyến: \(y=15\left(x+3\right)=15x+45\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=-15x+45\\y=15x+45\end{matrix}\right.\)