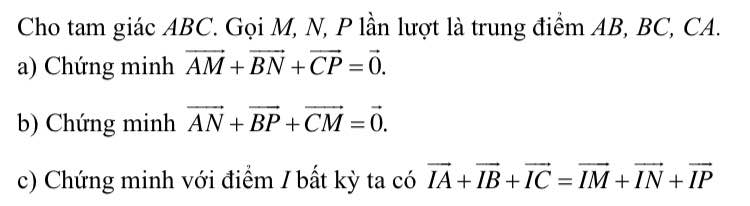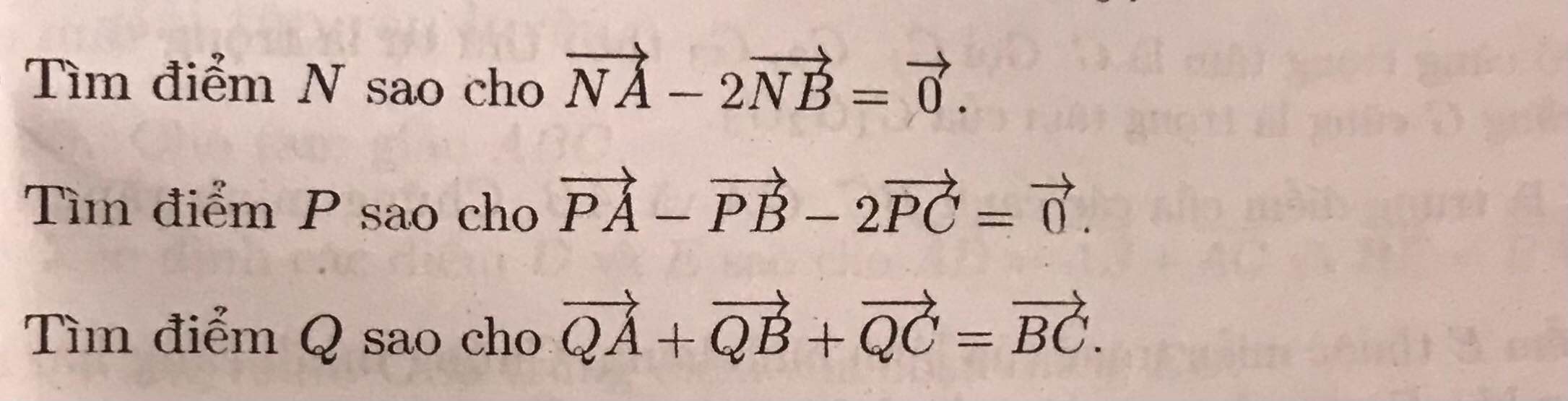Do M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
Tương tự ta có \(\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BC}\) ; \(\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{CA}\)
Do đó:
a.
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}=\overrightarrow{0}\)
b.
\(\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{AB}+\overrightarrow{BN}+\overrightarrow{BC}+\overrightarrow{CP}+\overrightarrow{CA}+\overrightarrow{AM}\)
\(=\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\right)+\left(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\right)=\left(\overrightarrow{AC}+\overrightarrow{CA}\right)+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
c.
\(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IM}+\overrightarrow{MA}+\overrightarrow{IN}+\overrightarrow{NB}+\overrightarrow{IP}+\overrightarrow{PC}\)
\(=\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP}-\left(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\right)\)
\(=\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP}-\overrightarrow{0}=\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP}\)