Học tại trường
Chưa có thông tin
Đến từ
Bình Định , Chưa có thông tin
Số lượng câu hỏi
47
Số lượng câu trả lời
155
Điểm GP
10
Điểm SP
78
Người theo dõi (14)
Đang theo dõi (8)

Câu trả lời:
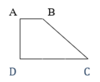
hình hơi xấu nhé bạn sorry


Câu trả lời:
28,26, tick cho mih nhe

Câu trả lời:
9
làm bạn mình na...na

Câu trả lời:
đề là j vậy bạn

Câu trả lời:
đề là j vậy bạn