Trong trường hợp 1-chiều, Định lý Lagrange cho ta khẳng định rằng:
Nếu hàm khả vi  có đạo hàm
có đạo hàm

thì  là hàm hằng.
là hàm hằng.
Tổng quát hơn, ta xét  là hàm suy rộng trên
là hàm suy rộng trên  và đạo hàm suy rộng của nó là hàm suy rộng
và đạo hàm suy rộng của nó là hàm suy rộng 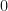 thì
thì  là hàm suy rộng hằng.
là hàm suy rộng hằng.
Một cách tương tự cho hàm và hàm suy rộng xác định trên miền (mở+liên thông) trong không gian  Các bạn thử cụ thể việc tương tự này xem sao?
Các bạn thử cụ thể việc tương tự này xem sao?
Quay trở lại trường hợp 1-chiều, hàm lồi trên toàn đường thẳng và bị chặn trên là hàm hằng.
Nhắc lại khái niệm hàm lồi:
 được gọi là hàm lồi nếu
được gọi là hàm lồi nếu
với mọi cặp điểm  ta đều có
ta đều có

Nếu hàm khả vi đến cấp 2 ta có thể phát biểu như sau:
Cho  khả vi đến cấp 2 và đạo hàm cấp 2 của nó
khả vi đến cấp 2 và đạo hàm cấp 2 của nó

Khi đó nếu  bị chặn trên, nghĩa là có số
bị chặn trên, nghĩa là có số  để
để

thì  là hàm hằng.
là hàm hằng.
Tuy nhiên có nhiều hàm lồi không có đạo hàm đến cấp 2, chẳng hạn  hay các hàm có đồ thị tuyến tính từng khúc. Tuy nhiên L. Schwartz chứng minh được rằng
hay các hàm có đồ thị tuyến tính từng khúc. Tuy nhiên L. Schwartz chứng minh được rằng
 là hàm lồi khi và chỉ khi nó có đạo hàm suy rộng cấp hai
là hàm lồi khi và chỉ khi nó có đạo hàm suy rộng cấp hai  là độ đo Radon, nghĩa là hàm suy rộng dương
là độ đo Radon, nghĩa là hàm suy rộng dương

hay

Ta có thể thấy điều này qua ví dụ  có
có  , hay
, hay 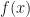 có đồ thị tuyến tính từng khúc có
có đồ thị tuyến tính từng khúc có

với  là hoành độ điểm gãy,
là hoành độ điểm gãy,  là độ lệch giữa hệ số góc của đoạn phải và đoạn trái được nối với nhau tại điểm
là độ lệch giữa hệ số góc của đoạn phải và đoạn trái được nối với nhau tại điểm  .
.
Một cách tương tự các bạn thử phát biểu cho hàm lõm. Hàm vừa lồi vừa lõm là hàm afin, nghĩa là

Khi đó nếu  bị chặn hoặc trên, hoặc dưới thì nó là hàm hằng.
bị chặn hoặc trên, hoặc dưới thì nó là hàm hằng.
Chú ý rằng, theo Bổ đề Weyl, đạo hàm cấp hai  ở trên có thể hiểu theo nghĩa suy rộng, nghĩa là ta chỉ cần giả sử
ở trên có thể hiểu theo nghĩa suy rộng, nghĩa là ta chỉ cần giả sử  có
có

Khi đó nếu  thì nó là hàm hằng.
thì nó là hàm hằng.
Phần tiếp theo của bài viết quan tâm đến: với các điều kiện gì đặt lên các đạo hàm riêng cấp 1, cấp 2 của hàm xác định trên toàn  thì hàm là hàm hằng? Trả lời câu hỏi này ta thu được các Định lý kiểu Liouville.
thì hàm là hàm hằng? Trả lời câu hỏi này ta thu được các Định lý kiểu Liouville.
Ta bắt đầu với các điều kiện đặt lên đạo hàm riêng cấp 1 và  Chú ý ta có thể coi
Chú ý ta có thể coi  theo cách
theo cách  Ta quan tâm đến các hàm
Ta quan tâm đến các hàm  . Ta có các đạo hàm riêng
. Ta có các đạo hàm riêng
 ,
,
 ,
,
với 
Đến đây ta gặp khái niệm tựa chính quy (quasiregular) sau:
Hàm  được gọi là tựa chính quy nếu
được gọi là tựa chính quy nếu

với hằng số 
Khi đó ta có kết quả sau:
Nếu hàm tựa chính quy  thỏa mãn:
thỏa mãn:

thì  là hàm hằng.
là hàm hằng.
Đặc biệt, khi hàm tựa chính quy bị chặn thì nó là hàm hằng.
Để chuyển sang trường hợp  ta cần quan sát điều kiện tựa chính quy. Để ý:
ta cần quan sát điều kiện tựa chính quy. Để ý:
-) Jacobien
 ,
,
-) chuẩn của đạo ánh

-) và

nên  là tựa chính quy khi và chỉ khi
là tựa chính quy khi và chỉ khi

hay

hoặc

với hằng số  .
.
Giờ ta có thể định nghĩa hàm tựa chính quy trong  như sau:
như sau:
Hàm  thỏa mãn
thỏa mãn

với hằng số 
được gọi là hàm tựa chính quy.
Nhắc lại
-) ma trận đạo ánh Jacobi 
-) chuẩn của ma trận đạo ánh Jacobi

-) định thức Jacobien của ma trận đạo ánh Jacobi

Khi đó ta cũng có

với hằng số 
Đặt  lần lượt là số nhỏ nhất trong các
lần lượt là số nhỏ nhất trong các  thỏa mãn (1), (2).
thỏa mãn (1), (2).
Trong trường hợp  ta có
ta có 
Ta có kết quả sau cho hàm tựa chính quy trong  như sau:
như sau:
Cho  là hàm tựa chính quy thỏa mãn
là hàm tựa chính quy thỏa mãn

với  Khi đó
Khi đó  là hàm hằng.
là hàm hằng.
Đặc biệt, nếu hàm tựa chính quy bị chặn thì nó là hàm hằng.
Trong trường hợp  , hàm tựa chính quy với hằng số
, hàm tựa chính quy với hằng số  hay
hay  , theo Bổ đề Weyl, là hàm chỉnh hình. Khi đó từng thành phần của nó đều là hàm điều hòa. Ta gặp lại Định lý Liouville cho hàm chỉnh hình trên
, theo Bổ đề Weyl, là hàm chỉnh hình. Khi đó từng thành phần của nó đều là hàm điều hòa. Ta gặp lại Định lý Liouville cho hàm chỉnh hình trên  cũng như hàm điều hòa trên mặt phẳng.
cũng như hàm điều hòa trên mặt phẳng.
Chú ý rằng hàm điều hòa là nghiệm của phương trình Laplace, trường hợp đặc biệt của phương trình elliptic. Phần tiếp ta quan tâm đến nghiệm  của phương trình elliptic, theo nghĩa suy rộng,
của phương trình elliptic, theo nghĩa suy rộng,

trong đó  là các hàm đo được thỏa mãn
là các hàm đo được thỏa mãn


trong đó  là các hằng số dương.
là các hằng số dương.
Khi đó nếu  thì nó là hàm hằng.
thì nó là hàm hằng.
Ta quan sát lại bài viết:
– bắt đầu xét hàm  ,
,
– mở rộng  ,
,
– rồi  và
và  ,
,
– quay trở lại 
Tiếp đến ta quan tâm đến nghiệm theo nghĩa suy rộng  của hệ phương trình elliptic
của hệ phương trình elliptic

với 
và hệ số  thỏa mãn
thỏa mãn

Khi đó, nếu  có độ tăng không quá đa thức, nghĩa là
có độ tăng không quá đa thức, nghĩa là

thì  là đa thức bậc
là đa thức bậc  nghĩa là từng thành phần của nó là đa thức bậc
nghĩa là từng thành phần của nó là đa thức bậc 
Đặc biệt nếu  thì nó là hằng số.
thì nó là hằng số.
Nhắc lại:  được gọi là nghiệm của hệ (3) nếu
được gọi là nghiệm của hệ (3) nếu

Vừa rồi ta xét các hàm xác định trên toàn không gian  Trở lại đầu bài các hàm chỉ cần xác định trên miền (mở+liên thông). Cũng cần chú ý việc xác định trên toàn không gian là rất cần qua ví dụ:
Trở lại đầu bài các hàm chỉ cần xác định trên miền (mở+liên thông). Cũng cần chú ý việc xác định trên toàn không gian là rất cần qua ví dụ:
– hàm  là nghiệm bị chặn, khác hằng, của phương trình Laplace ngoài hình tròn đơn vị.
là nghiệm bị chặn, khác hằng, của phương trình Laplace ngoài hình tròn đơn vị.
Phần cuối của bài viết ta quay trở lại xét hàm  là miền trong
là miền trong  H. Brezis là người đầu tiên đưa ra các điều kiện thú vị dạng tích phân như sau:
H. Brezis là người đầu tiên đưa ra các điều kiện thú vị dạng tích phân như sau:
Hàm đo được  thỏa mãn
thỏa mãn

thì  là hàm hằng.
là hàm hằng.
Tổng quát hơn một chút, với  nếu hàm đo được
nếu hàm đo được  thỏa mãn
thỏa mãn

thì  là hàm hằng.
là hàm hằng.
Tổng quát hơn nữa như sau:
Cho họ hàm  gồm các hàm đo được
gồm các hàm đo được  thỏa mãn
thỏa mãn


và hàm lồi  thỏa mãn
thỏa mãn

Khi đó nếu hàm đo được  thỏa mãn
thỏa mãn

thì  là hàm hằng.
là hàm hằng.
Nếu lấy  và
và

ta sẽ có kết quả ngay trên.
R. Ignat lại quan tâm đến vấn đề sau:
Xét tập
 .
.
Tìm điều kiện cần và đủ cho một hàm  để
để
với bất kỳ hàm đo được  thỏa mãn
thỏa mãn

thì  là hàm hằng.
là hàm hằng.
Ignat đưa ra các điều kiện như sau:
– Điều kiện cần: 
– Điều kiện đủ:














