Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
53
Số lượng câu trả lời
43
Điểm GP
1
Điểm SP
2
Người theo dõi (1)

Đang theo dõi (1)

Chủ đề:
Chương 2: HÀM SỐ LŨY THỪA. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARITCâu hỏi:
Cho \(x\), \(y\), \(z\) \(\in\left[0;2\right]\) và thỏa mãn \(x+2y+z=6\). Tìm giá trị lớn nhất của biểu thức \(P=3^{2x-x^2}+5^{2y-y^2}+3^z+2x^2+4y^2\)
A. \(maxP=25\) B. \(maxP=26\)
C. \(maxP=27\) D. \(maxP=30\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥
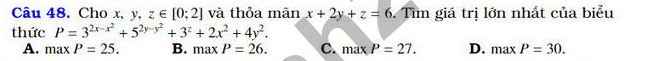

Chủ đề:
Chương 1:ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐCâu hỏi:
Cho hàm số \(f\left(x\right)\) xác định trên \(R\), có đạo hàm \(f'\left(x\right)=\left(x^2-4\right)\left(x-5\right)\forall x\in R\) và \(f\left(1\right)=0\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left(x\right)=\left|f\left(x^2+1\right)-m\right|\) có nhiều điểm cực trị nhất?
A.7 B. 8 C. 5 D. 6





Câu trả lời:
3. A 4B 5.C

Chủ đề:
Chương 4: SỐ PHỨCCâu hỏi:
Cho hai số phức \(z\) và \(w\) thay đổi thỏa mãn các điều kiện \(\left|z+1+i\right|=\left|z\right|\) và \(\left|w-3-4i\right|=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\left|z-w-1-i\right|\)
A.\(minP=5\sqrt{2}\) B. \(minP=5\sqrt{2}-1\) C. \(minP=3\sqrt{2}\) D. \(minP=3\sqrt{2}-1\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥



Chủ đề:
Chương 3: NGUYÊN HÀM. TÍCH PHÂN VÀ ỨNG DỤNGCâu hỏi:
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}2\sin^2x+1,x< 0\\2^x;x\ge0\end{matrix}\right.\). Giả sử \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(R\) và thỏa mãn điều kiện \(F\left(1\right)=\dfrac{2}{ln2}\). Tính \(F\left(-\pi\right)\)
A. \(F\left(-\pi\right)=-2\pi+\dfrac{1}{ln2}\) B. \(F\left(-\pi\right)=-2\pi-\dfrac{1}{ln2}\)
C. \(F\left(-\pi\right)=-\pi-\dfrac{1}{ln2}\) D. \(F\left(-\pi\right)=-2\pi\)
Mình cần bài giải ạ, mình cảm ơn nhiều ♥





