Bài 9: Thể tích hình chóp đều

1. Công thức tính thể tích

Có hai dụng cụ đựng nước hình lăng trụ đứng và hình chóp đều có các đáy là các đa giác đều có thể đặt chồng khít lên nhau. Chiều cao của lăng trụ bằng chiều cao của hình chóp:

Nếu ta lấy dụng cụ hình chóp đều múc đầy nước rồi đổ vào lăng trụ đứng thì ta thấy chiều cao cột nước này chỉ bằng \(\dfrac{1}{3}\) chiều cao của lăng trụ. 

Như vậy: V_chóp = \(\dfrac{1}{3}\).V_{lăng trụ}

Bài trước ta đã biết: V_{lăng trụ} = \(S\).\(h\)

Trong đó: \(S\) là diện tích đáy ;

                \(h\) là chiều cao lăng trụ đứng.

Do đó: V_chóp = \(\dfrac{1}{3}\).\(S\).\(h\)

Người ta chứng minh được công thức trên đúng với mọi hình chóp đều.

Ta có công thức tính thể tích hình chóp đều là:

                \(V=\dfrac{1}{3}.S.h\)

     Trong đó: ​\(S\) ​là diện tích đáy ; ​\(h\) ​là chiều cao hình chóp đều.

2. Các ví dụ

Ví dụ 1: Cho một hình chóp tam giác đều có chiều cao \(6cm\) và bán kính đường tròn ngoại tiếp tam giác đáy cũng là ​\(6cm\). Tính thể tích hình chóp đều? Biết \(\sqrt{3}\approx1,73\)​

Giải: 

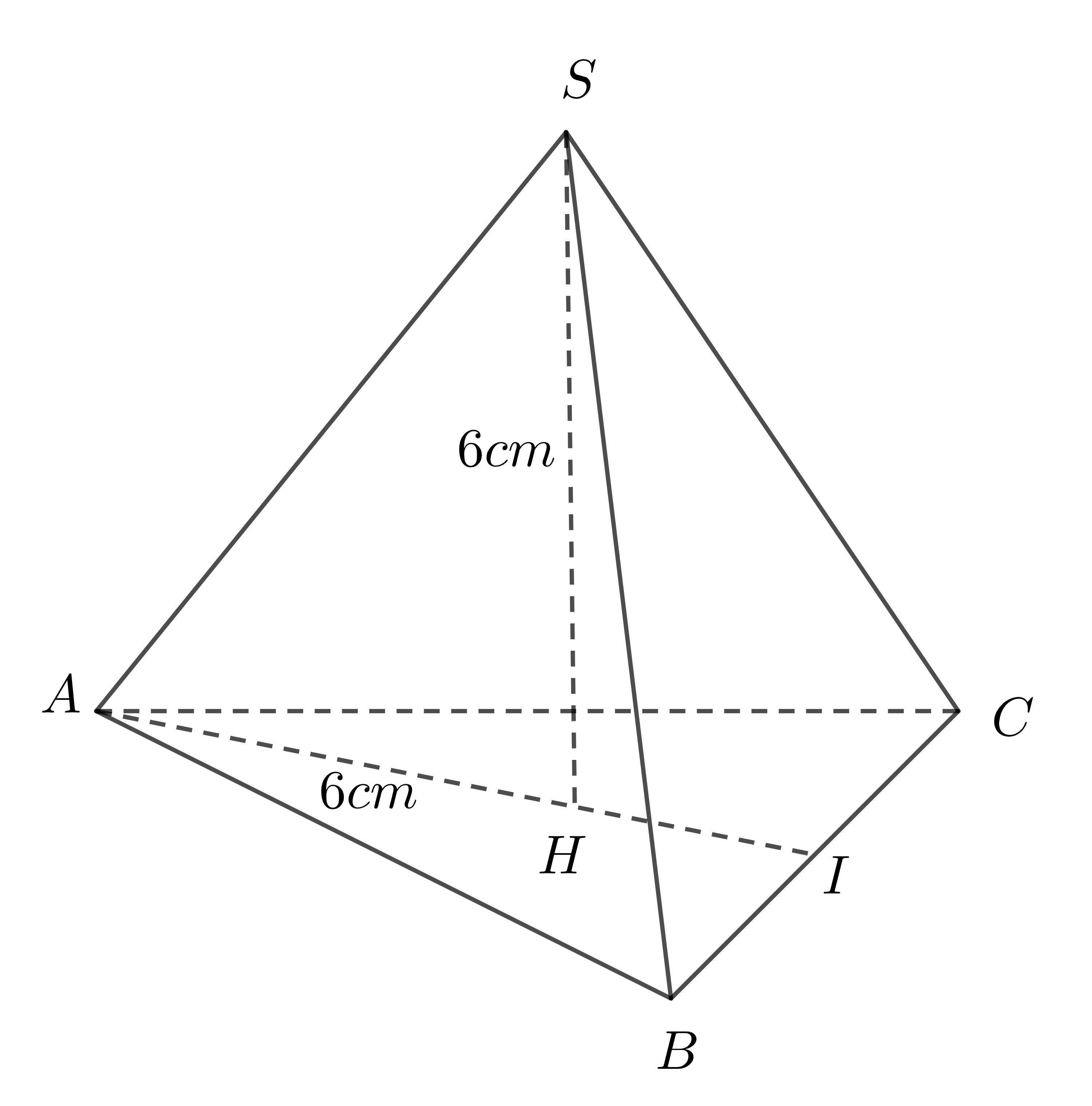
Xét hình chóp tam giác đều \(S.ABC\) có đường cao \(SH=6cm\) thì \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\)

Do \(\Delta ABC\) đều, có bán kính đường tròn ngoại tiếp là \(R=6cm\)

Nên độ dài cạnh tam giác đáy là: 

                       \(a=R\sqrt{3}=6\sqrt{3}\left(cm\right)\)

Diện tích tam giác đáy là: 

                      \(S=\dfrac{a^2\sqrt{3}}{4}=\dfrac{\left(6\sqrt{3}\right)^2.\sqrt{3}}{4}=27\sqrt{3}\left(cm^2\right)\)

Thể tích của hình chóp là: 

                     \(V=\dfrac{1}{3}Sh=\dfrac{1}{3}.27\sqrt{3}.6\approx93,42\left(cm^3\right)\)

Ví dụ 2: Cho hình chóp tứ giác đều có độ dài cạnh đáy là \(5cm\), chiều cao \(9cm\).

      a) Tính độ dài cạnh bên hình chóp?

      b) Tính thể tích hình chóp tứ giác trên?

Giải:

a) Xét hình chóp tứ giác đều \(S.ABCD\) có độ dài cạnh đáy \(AB=BC=CD=DA=5cm\) và chiều cao \(SH=9cm\)

Do \(H\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\) nên \(H\) là giao điểm 2 đường chéo \(AC,BD\).

Ta có \(\Delta BCD\) vuông cân tại \(C\). Áp dụng định lí Py-ta-go ta có: \(BC^2+CD^2=BD^2\)

\(\Rightarrow BD=\sqrt{BC^2+CD^2}=\sqrt{5^2+5^2}=5\sqrt{2}\left(cm\right)\)

\(\Rightarrow HB=HD=\dfrac{BC}{2}=\dfrac{5\sqrt{2}}{2}\left(cm\right)\)

Áp dụng Py-ta-go trong \(\Delta SHB\) ta có: \(SH^2+HB^2=SB^2\)

\(\Rightarrow SB=\sqrt{SH^2+HB^2}=\sqrt{9^2+\left(\dfrac{5\sqrt{2}}{2}\right)^2}\approx9,67\left(cm\right)\)

Vậy hình chóp tứ giác đều có độ dài cạnh bên \(\approx9,67cm\)

b) Diện tích đáy là: \(S=5.5=25\left(cm^2\right)\)

    Thể tích hình chóp đều là: \(V=\dfrac{1}{3}Sh=\dfrac{1}{3}.25.9=75\left(cm^3\right)\)

Ví dụ 3: Cho hình chóp tứ giác đều có độ dài cạnh đáy là \(8cm\), trung đoạn là \(10cm\). Tính diện tích xung quanh và thể tích hình chóp?

Giải:

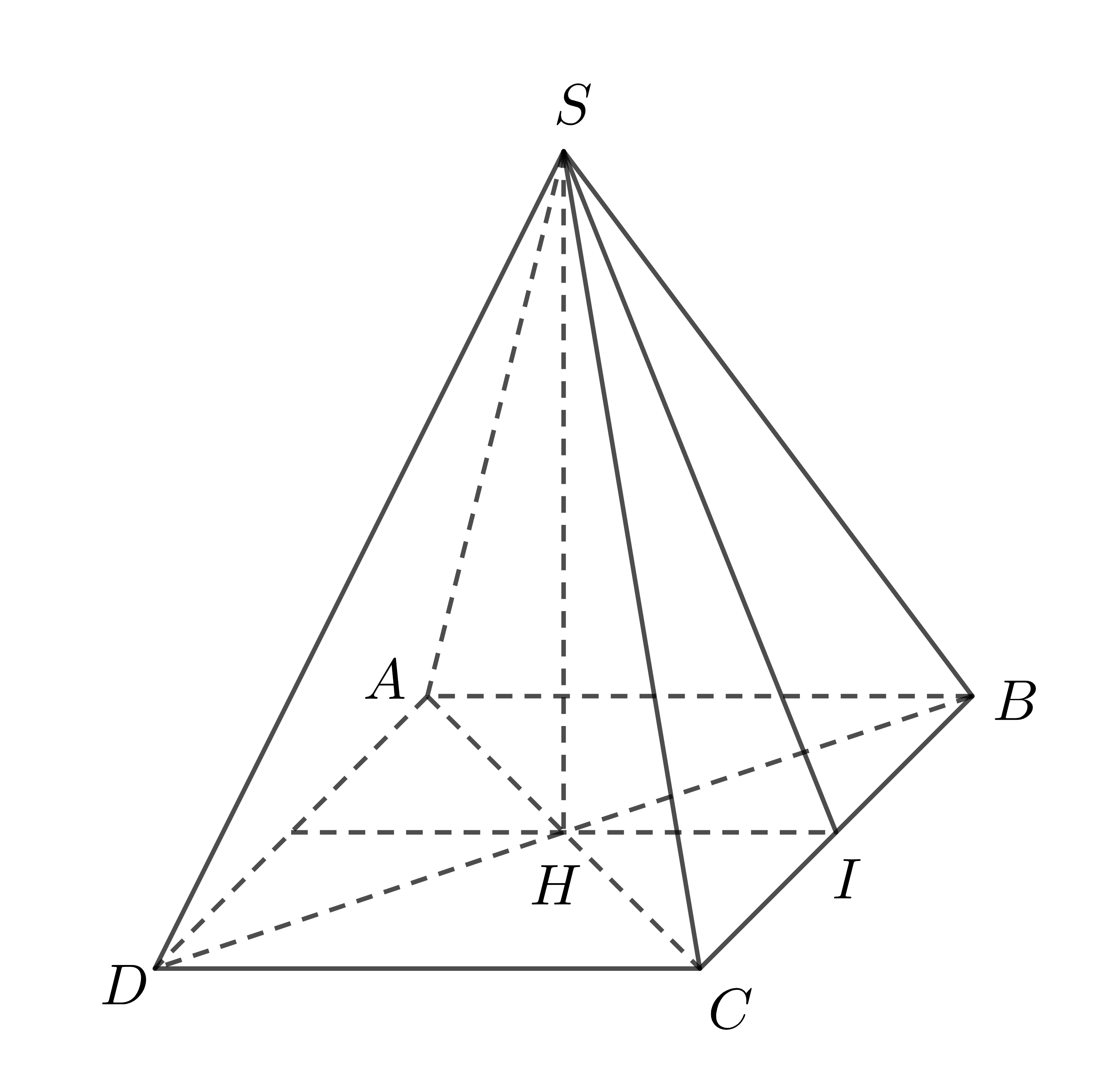
Xét hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy \(AB=BC=CD=DA=8cm\), trung đoạn \(SI=10cm\), đường cao \(SH\)

\(\Delta ABC\) có \(H,I\) lần lượt là trung điểm \(AC,BC\)

Nên \(HI\) là đường trung bình của \(\Delta ABC\) \(\Rightarrow HI=\dfrac{1}{2}AB=\dfrac{1}{2}.8=4\left(cm\right)\)

Ta có: \(\Delta SHI\) vuông tại \(H\). Áp dụng định lý Py-ta-go ta có: \(SH^2+HI^2=SI^2\)

\(\Rightarrow SH^2=SI^2-HI^2\) \(\Rightarrow SH=\sqrt{10^2-4^2}=2\sqrt{21}\left(cm\right)\)

Chu vi đáy là: \(8.4=32\left(cm\right)\)

Diện tích xung quanh hình chóp là: \(S_{xq}=\dfrac{32}{2}.10=160\left(cm^2\right)\)

Diện tích đáy là: \(S=8.8=64\left(cm^2\right)\)

Thể tích hình chóp là: \(V=\dfrac{1}{3}Sh=\dfrac{1}{3}.64.2\sqrt{21}=\dfrac{256}{3}\sqrt{21}\approx391,05\left(cm^3\right)\)