Bài 2. Con lắc lò xo
Nội dung lý thuyết
CON LẮC LÒ XO
1. Con lắc lò xo

- Con lắc lò xo gồm một vật nặng khối lượng m (kg) gắn vào một lò xo có độ cứng k (N/m) và có khối lượng không đáng kể
- Vị trí cân bằng của vật là vị trí mà lò xo không biến dạng
- Kéo vật ra khỏi vị trí cân bằng cho lò xo dãn rồi buông tay ta thấy vật dao động trên một đoạn thẳng quanh vị trí cân bằng
- Nếu bỏ qua ma sát thì dao động của vật m (hay của con lắc lò xo) là một dao động điều hòa.
2. Khảo sát dao động của con lắc lò xo về mặt động lực học

- Ở vị trí vật có li độ \(x\) thì độ biến dạng của lò xo \(\Delta l=x\)
Lực đàn hồi khi đó là \(F=-kx\)
- Áp dụng định luật II Newton ta có
\(a=-\dfrac{k}{m}x\)
Đặt \(\omega^2=\frac{k}{m}\) thì ta có \(a=-\omega^2x\)
\(\Rightarrow\) Dao động của con lắc lò xo là dao động điều hòa với
\(\omega=\sqrt{\frac{k}{m}}\) và \(T=2\pi\sqrt{\frac{m}{k}}\)
- Lực luôn hướng về vị trí cân bằn gọi là lực kéo về

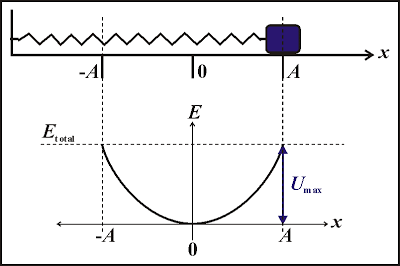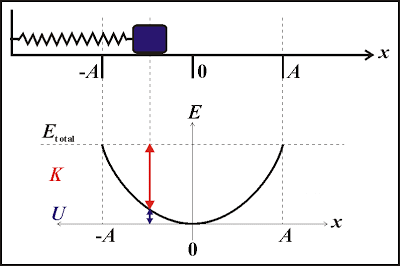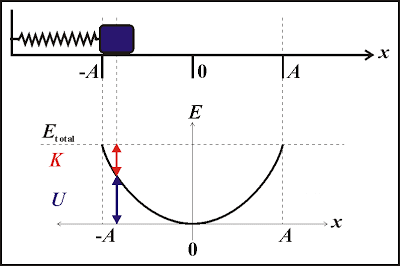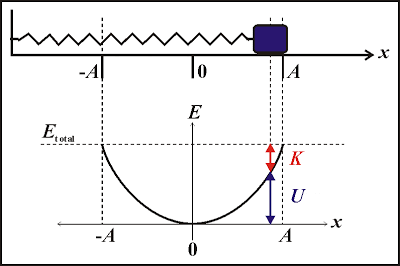
3. Khảo sát dao động của con lắc lò xo về mặt năng lượng
- Động năng của con lắc lò xo
\(W=\frac{1}{2}mv^2\)
- Thế năng của con lắc lò xo
\(W_t=\frac{1}{2}kx^2\)
- Cơ năng của con lắc lò xo
\(W=W_đ+W_t=\frac{1}{2}mv^2+\frac{1}{2}kx^2\)
Chứng minh được rằng
\(W=\frac{1}{2}kA^2=const\)
Cơ năng của con lắc tỉ lệ với bình phương biên độ
Cơ năng của con lắc được bảo toàn nếu bỏ qua ma sát