Bài 11: Tính chất cơ bản của phép nhân phân số
Các câu hỏi tương tự
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số
Ví dụ : Tính chất giao hoán của phép nhân phân số :
dfrac{a}{b}.dfrac{c}{d}dfrac{a.c}{b.d}dfrac{c.a}{d.b}dfrac{c}{d}.dfrac{a}{b}
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên ?
Đọc tiếp
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số
Ví dụ : Tính chất giao hoán của phép nhân phân số :
\(\dfrac{a}{b}.\dfrac{c}{d}=\dfrac{a.c}{b.d}=\dfrac{c.a}{d.b}=\dfrac{c}{d}.\dfrac{a}{b}\)
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên ?
viết các số đo thời gian sau với đơn vị là giờ (chú ý rút gọn nếu có thể)
a)10 phút b)35 phút c)40 phút d)9 phút e)150 phút g)20 phút
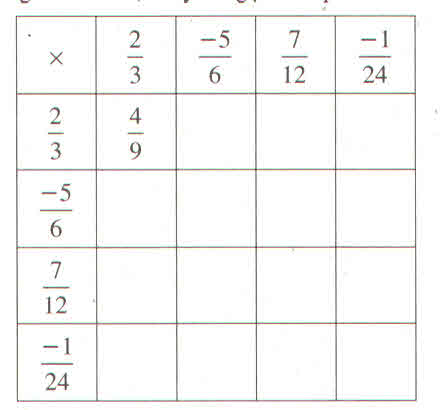
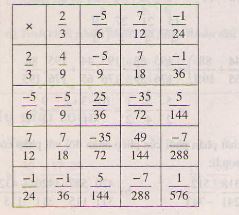
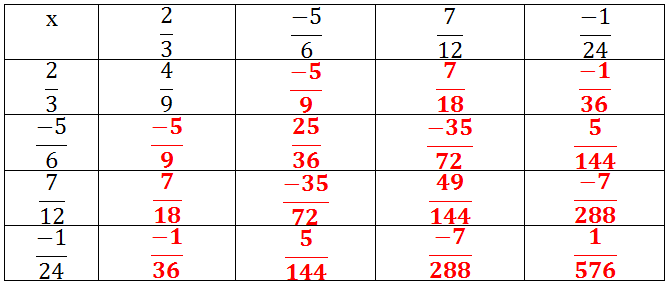
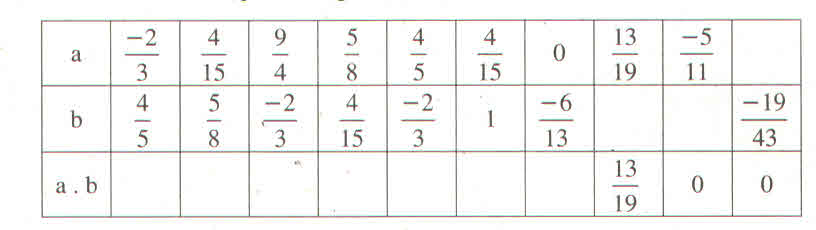
Điền các số thích hợp vào bảng sau :
Trong hai câu sau đây, câu nào đúng ?
Câu thứ nhất : Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu
Câu thứ hai : Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}dfrac{1}{3}.dfrac{1}{2}.dfrac{1}{5} (B) left(dfrac{1}{3}.dfrac{1}{5}right).dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}.dfrac{1}{2}right)
(C) dfrac{1}{3}.dfrac{1}{5}+dfrac{1}{3}.dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}+dfrac{1}{2}right) (D) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}left(dfrac{1}{3}.dfrac{1}{5}right).left(dfr...
Đọc tiếp
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{5}\) (B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
(C) \(\dfrac{1}{3}.\dfrac{1}{5}+\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}+\dfrac{1}{2}\right)\) (D) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\left(\dfrac{1}{3}.\dfrac{1}{2}\right)\)
Hãy chọn đáp án đúng ?
rút gọn:
a,121.75.130.169/39.60.11.198
b,3010.(-5)21/115.138
Khi giặt, vải bị co đi \(\dfrac{1}{16}\) theo chiều dài và \(\dfrac{1}{18}\) theo chiều rộng. Hỏi cần phải mua bao nhiêu mét vải khổ 80cm để sau khi giặt có \(17m^2\) ?
Bài 1 : Tìm STN có 3 chữ số abc , biết rằng b2= a.c và abc - cba=495.
Bài 2 : Rút gọn : 52 . 611 . 162 + 62 . 126 . 152 / 2 . 612. 104- 812 . 960
Bài 3 : Tìm STN để phân số 6n + 99/ 3n + 4 là :
a ) Số tự nhiên
b ) Phân số tối giản
Áp dụng các tính chất của phép nhân phân số để tính nhanh :
\(M=\dfrac{8}{3}.\dfrac{2}{5}.\dfrac{3}{8}.10.\dfrac{19}{92}\)
\(N=\dfrac{5}{7}.\dfrac{5}{11}+\dfrac{5}{7}.\dfrac{2}{11}-\dfrac{5}{7}.\dfrac{14}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right).\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)