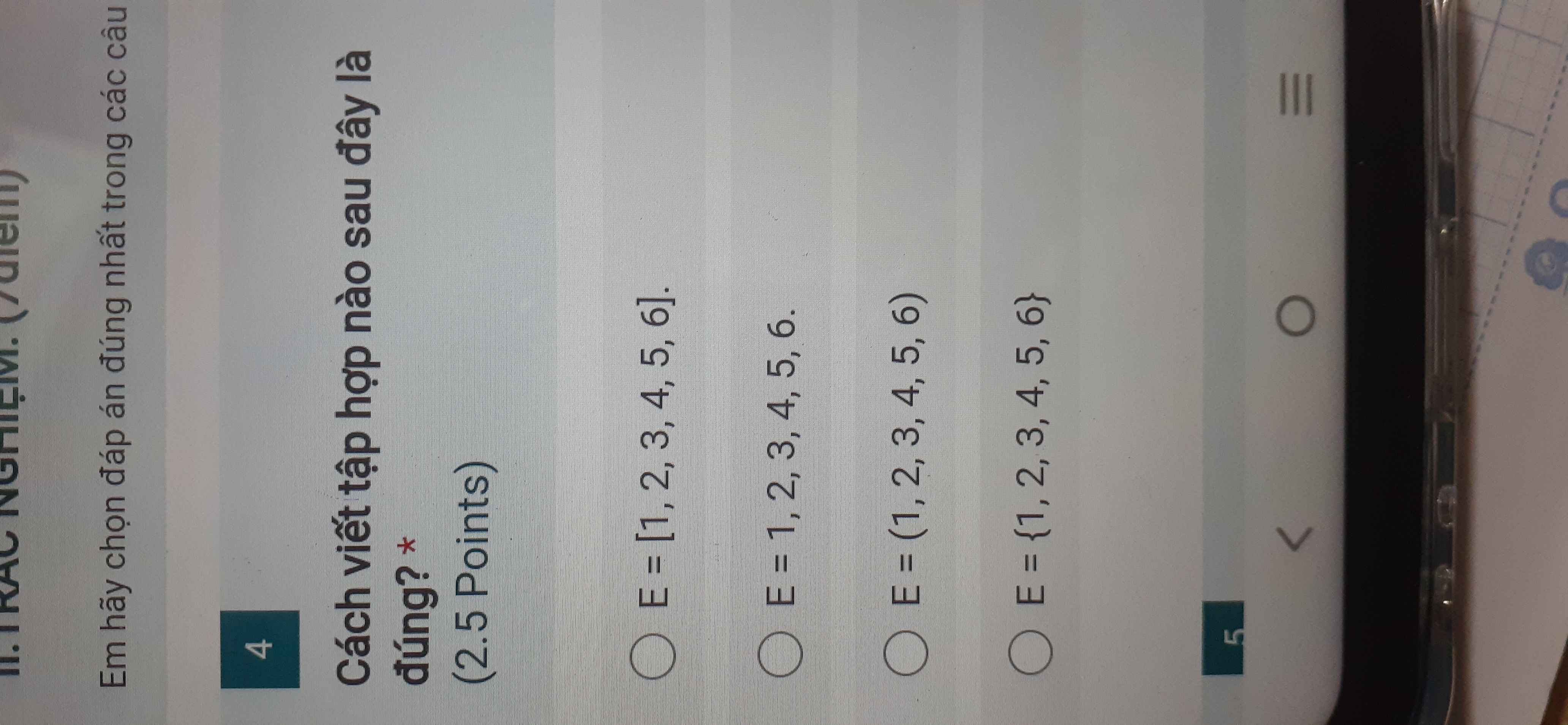
Ta có:
100A=\(\dfrac{100^{2022}+100}{100^{2022}+1}\); 100B=\(\dfrac{100^{2021}+100}{100^{2021}+1}\)
100A=\(\dfrac{100^{2022}+1+99}{100^{2022}+1}\); 100B=\(\dfrac{100^{2021}+1+99}{100^{2021}+1}\)
100A=1+\(\dfrac{99}{100^{2022}+1}\);100B=1+\(\dfrac{99}{100^{2021}+1}\)
Ta có:\(100^{2022}+1\)>\(100^{2021}+1\)
=>\(\dfrac{99}{100^{2022}+1}\)<\(\dfrac{99}{100^{2021}+1}\)
=>\(\dfrac{100^{2022}+100}{100^{2022}+1}\)<\(\dfrac{100^{2021}+100}{100^{2021}+1}\)
=>100A<100B
=>A<B

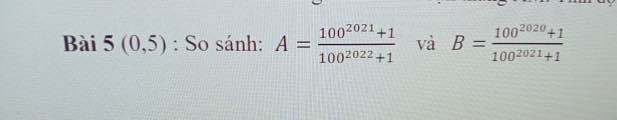 Giúp
Giúp