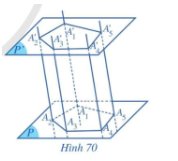
Cho hai mặt phẳng song song (P) và (P’).Trongmặtphẳng (P),chođagiác A1A2...An .Qua các đỉnh A1,A2,...,A vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P) lần lượt tạiA1′,A2′,...,An′(Hình 70 minh họa cho trường hợp n = 5).
a) Các tứ giácA1A2A2′A1′,A2A3A3′A2′,...,AnA1A1′An′ là những hình gì?
b) Các cạnh tương ứng của hai đa giácA1A2...AnvàA1′A2.′..Ancó đặc điểm gì?