Trên mặt đồng hồ ở Hình 1, quan sát hai góc: góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.
Hai góc đó có liên hệ gì đặc biệt?
Bài 1. Góc ở vị trí đặc biệt
Khởi động (SGK Cánh Diều trang 90)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều trang 90-92)
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Thảo luận (1)Hướng dẫn giải
Hoạt động 2 (SGK Cánh Diều trang 90-92)
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
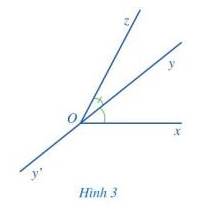
Thảo luận (1)Hướng dẫn giảia) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
b)
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Cánh Diều trang 90-92)
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
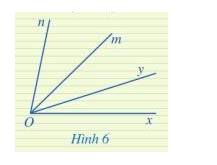
Thảo luận (1)Hướng dẫn giảiHai góc xOy và mOn không phải là hai góc kề nhau vì không có cạnh nào chung.
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Cánh Diều trang 90-92)
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
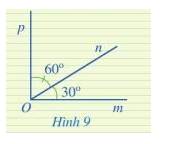
Thảo luận (1)Hướng dẫn giảiHai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Cánh Diều trang 92,93)
Tìm tổng số đo của góc 110 \(^\circ \) và 70 \(^\circ \)
Thảo luận (1)Hướng dẫn giải2 góc có tổng số đo là: 110 \(^\circ \)+70 \(^\circ \) = 180 \(^\circ \)
(Trả lời bởi Hà Quang Minh)
Hoạt động 4 (SGK Cánh Diều trang 92,93)
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
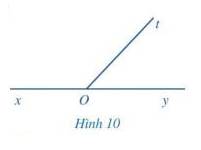
Thảo luận (1)Hướng dẫn giảia) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng
(Trả lời bởi Hà Quang Minh)
Luyện tập 3 (SGK Cánh Diều trang 92,93)
Tính góc xOt trong Hình 12
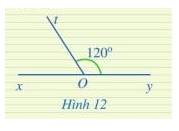
Thảo luận (1)Hướng dẫn giảiTa có: \(\widehat {xOt} + \widehat {tOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {xOt} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 5 (SGK Cánh Diều trang 93,94)
Quan sát hai góc xOz và yOt ở Hình 13, trong đó, Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:
a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.
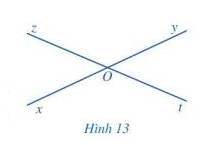
Thảo luận (1)Hướng dẫn giảia) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.
(Trả lời bởi Hà Quang Minh)
Hoạt động 6 (SGK Cánh Diều trang 93,94)
Quan sát Hình 15 và giải thích vì sao:
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\) và \(\widehat {xOy} = \widehat {zOt}\)
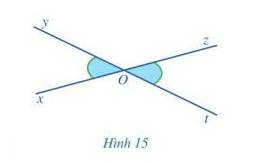
Thảo luận (1)Hướng dẫn giảia) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.
Vậy hai góc xOy và yOz là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz là hai tia đối nhau nên hai góc xOy và yOz là hai góc kề bù.
b) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.
Vậy hai góc yOz và zOt là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot là hai tia đối nhau nên hai góc yOz và zOt là hai góc kề bù.
c) Do
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = 180^\circ ;\\\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 180^\circ \end{array}\)
Vậy \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\)
\( \Rightarrow \widehat {xOy} = \widehat {zOt}\)
Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.
(Trả lời bởi Hà Quang Minh)