§2. Phương trình đường tròn
Nội dung lý thuyết
Các phiên bản khác1. Phương trình đường tròn có tâm và bán kính cho trước
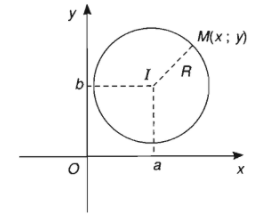
Trong mặt phẳng \(Oxy\) cho đường thẳng \(\left(C\right)\) tâm \(I\left(a;b\right)\), bán kính \(R\).
Ta có \(M\left(x;y\right)\in\left(C\right)\Leftrightarrow IM=R\)
\(\Leftrightarrow\sqrt{\left(x-a\right)^2+\left(y-b\right)^2}=R\)
\(\Leftrightarrow\left(x-a\right)^2+\left(y-b\right)^2=R^2\)
Phương trình \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) được gọi là phương trình đường tròn tâm \(I\left(a;b\right)\) bán kính \(R\).
Chẳng hạn, phương trình đường tròn tâm \(I\left(2;-3\right)\) bán kính \(R=5\) là: \(\left(x-2\right)^2+\left(y+3\right)^2=25\)
Ví dụ 1: Cho hai điểm \(A\left(1;2\right)\) và \(B\left(-3;4\right)\). Viết phương trình đường tròn \(\left(C\right)\) đường kính \(AB\).
Giải:
Gọi \(I\) là trung điểm của đoạn thẳng \(AB\). Ta có \(I\left(-1;3\right)\)
Bán kính của đường tròn \(\left(C\right)\) là \(IA=\sqrt{\left(-1-1\right)^2+\left(3-2\right)^2}=\sqrt{5}\)
Như vậy ta được đường tròn \(\left(C\right)\) tâm \(I\left(-1;3\right)\) bán kính \(R=\sqrt{5}\)
Suy ra phương trình đường tròn \(\left(C\right)\) là: \(\left(x+1\right)^2+\left(y-3\right)^2=5\).
Ví dụ 2: Viết phương trình đường tròn tâm \(I\left(2;-3\right)\) và đi qua điểm \(M\left(-2;3\right)\).
Giải:
Với \(I\left(2;-3\right)\), \(M\left(-2;3\right)\) ta có \(IM=\sqrt{\left(2+2\right)^2+\left(-3-3\right)^2}=\sqrt{52}\)
Đường tròn tâm \(I\) và đi qua điểm \(M\) có bán kính \(R=IM=\sqrt{52}\)
Do đó ta có phương trình đường tròn là: \(\left(x-2\right)^2+\left(y+3\right)^2=52\).
Ví dụ 3: Tìm tâm và bán kính của các đường tròn sau:
a) \(x^2+y^2-2x-2y-2=0\) ;
b) \(16x^2+16y^2+16x-8y-11=0\)
Giải:
a) Ta có: \(x^2+y^2-2x-2y-2=0\) \(\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2=4\)
Vậy đường tròn này có tâm \(I\left(1;1\right)\) và bán kính \(R=2\).
b) Ta có: \(16x^2+16y^2+16x-8y-11=0\)
\(\Leftrightarrow x^2+y^2+x-\dfrac{1}{2}y-\dfrac{11}{16}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{4}\right)^2=1\)
Vậy đường tròn này có tâm \(I\left(-\dfrac{1}{2};\dfrac{1}{4}\right)\) bán kính \(R=1\).
Chú ý: Phương trình đường tròn có tâm là gốc toạ độ \(O\) và có bán kính \(R\) là:
\(x^2+y^2=R^2\)
@1972697@
2. Nhận xét
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) có thể được viết dưới dạng \(x^2+y^2-2ax-2by+c=0\) , trong đó \(c=a^2+b^2-R^2\).
Ngược lại, phương trình \(x^2+y^2-2ax-2by+c=0\) là phương trình của đường tròn \(\left(C\right)\) khi và chỉ khi \(a^2+b^2-c>0\). Khi đó đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\) và bán kính \(R=\sqrt{a^2+b^2-c}\).
Ta xét lại ví dụ 3 trên nhưng với cách làm khác.
Ví dụ 3: Tìm tâm và bán kính của các đường tròn sau:
a) \(x^2+y^2-2x-2y-2=0\) ;
b) \(16x^2+16y^2+16x-8y-11=0\)
Giải:
a) Ta có \(x^2+y^2-2x-2y-2=0\) \(\Leftrightarrow\) \(x^2+y^2-2.1.x-2.1y-2=0\)
Suy ra phương trình trên có các hệ số \(a=1,b=1,c=-2\)
Nên đường tròn có tâm \(I\left(1;1\right)\) và bán kính \(R=\sqrt{1^2+1^2-\left(-2\right)}=\sqrt{4}=2\)
b) Ta có \(16x^2+16y^2+16x-8y-11=0\) \(\Leftrightarrow x^2+y^2+x-\dfrac{1}{2}y-\dfrac{11}{16}=0\)
\(\Leftrightarrow x^2+y^2-2.\dfrac{-1}{2}.x-2.\dfrac{1}{4}.y-\dfrac{11}{16}=0\)
Suy ra phương trình trên có các hệ số \(a=-\dfrac{1}{2},b=\dfrac{1}{4},c=-\dfrac{11}{16}\)
Nên đường tròn có tâm \(I\left(-\dfrac{1}{2};\dfrac{1}{4}\right)\), bán kính \(R=\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2-\left(-\dfrac{11}{16}\right)}=1\)
Ví dụ 4: Viết phương trình đường tròn \(\left(C\right)\) đi qua 3 điểm \(A\left(1;2\right)\), \(B\left(5;2\right)\) và \(C\left(1;-3\right)\).
Giải:
Gọi phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2-2ax-2by+c=0\)
Do \(A\left(1;2\right)\in\left(C\right)\) nên ta có \(1^2+2^2-2.a.1-2.b.2+c=0\) \(\Rightarrow2a+4b-c=5\) (1)
Do \(B\left(5;2\right)\in\left(C\right)\) nên ta có \(5^2+2^2-2.a.5-2.b.2+c=0\) \(\Rightarrow10a+4b-c=29\) (2)
Do \(C\left(1;-3\right)\in\left(C\right)\) nên ta có \(1^2+\left(-3\right)^2-2.a.1-2.b.\left(-3\right)+c=0\) \(\Rightarrow2a-6b-c=10\) (3)
Từ (1), (2) và (3) ta có hệ phương trình \(\left\{{}\begin{matrix}2a+4b-c=5\\10a+4b-c=29\\2a-6b-c=10\end{matrix}\right.\)
Giải hệ phương trình trên ta được nghiệm \(a=3,b=-\dfrac{1}{2},c=-1\)
Thay vào ta được phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2-6x+y-1=0\).
@1972874@
3. Phương trình tiếp tuyến của đường tròn
Cho điểm \(M_0\left(x_0;y_0\right)\) nằm trên đường tròn \(\left(C\right)\) tâm \(I\left(a;b\right)\).
Gọi \(\Delta\) là tiếp tuyến với \(\left(C\right)\) tại \(M_0\).
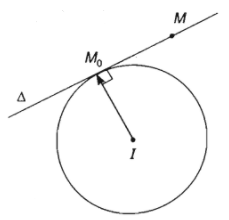
Ta có \(M_0\) thuộc \(\Delta\) và vectơ \(\overrightarrow{IM_0}=\left(x_0-a;y_0-b\right)\) là vectơ pháp tuyến của \(\Delta\).
Do đó \(\Delta\) có phương trình là:
\(\left(x_0-a\right)\left(x-x_0\right)+\left(y_0-b\right)\left(y-y_0\right)=0\) (2)
Phương trình (2) là phương trình tiếp tuyến của đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) tại điểm \(M_0\) nằm trên đường tròn.
Ví dụ 5: Viết phương trình tiếp tuyến tại điểm \(M\left(3;4\right)\) thuộc đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-2\right)^2=8\).
Giải:
Từ phương trình \(\left(x-1\right)^2+\left(y-2\right)^2=8\) ta suy ra \(\left(C\right)\) có tâm \(I\left(1;2\right)\)
Suy ra phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là
\(\left(3-1\right)\left(x-3\right)+\left(4-2\right)\left(y-4\right)=0\)
\(\Leftrightarrow2x+2y-14=0\)
\(\Leftrightarrow x+y-7=0\)
Vậy phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là \(x+y-7=0\).
@1974034@