§2. Tổng và hiệu của hai vectơ
Nội dung lý thuyết
Các phiên bản khác1. Tổng của hai vectơ
Định nghĩa:
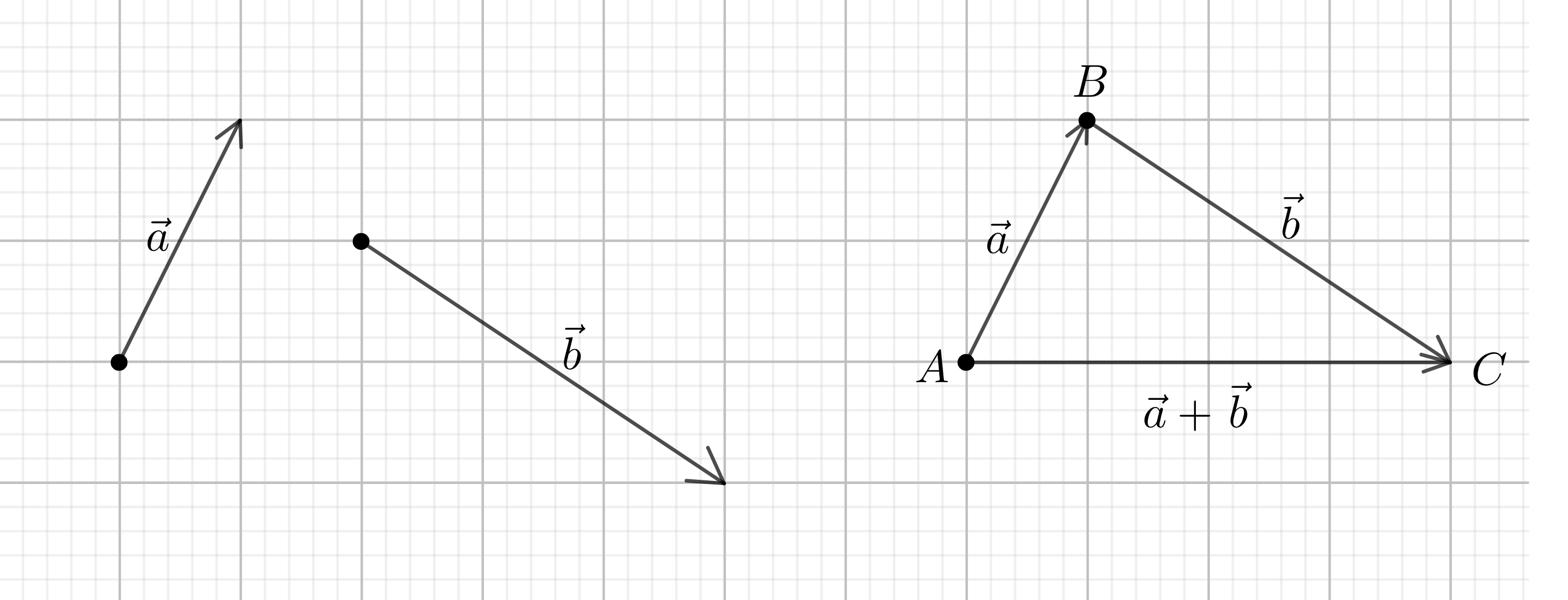
Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Lấy một điểm \(A\) tuỳ ý, vẽ \(\overrightarrow{AB}=\overrightarrow{a}\) và \(\overrightarrow{BC}=\overrightarrow{b}\). Vectơ \(\overrightarrow{AC}\) được gọi là tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\).
Ta kí hiệu tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là \(\overrightarrow{a}+\overrightarrow{b}\). Vậy \(\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}\).
Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.
2. Quy tắc hình bình hành
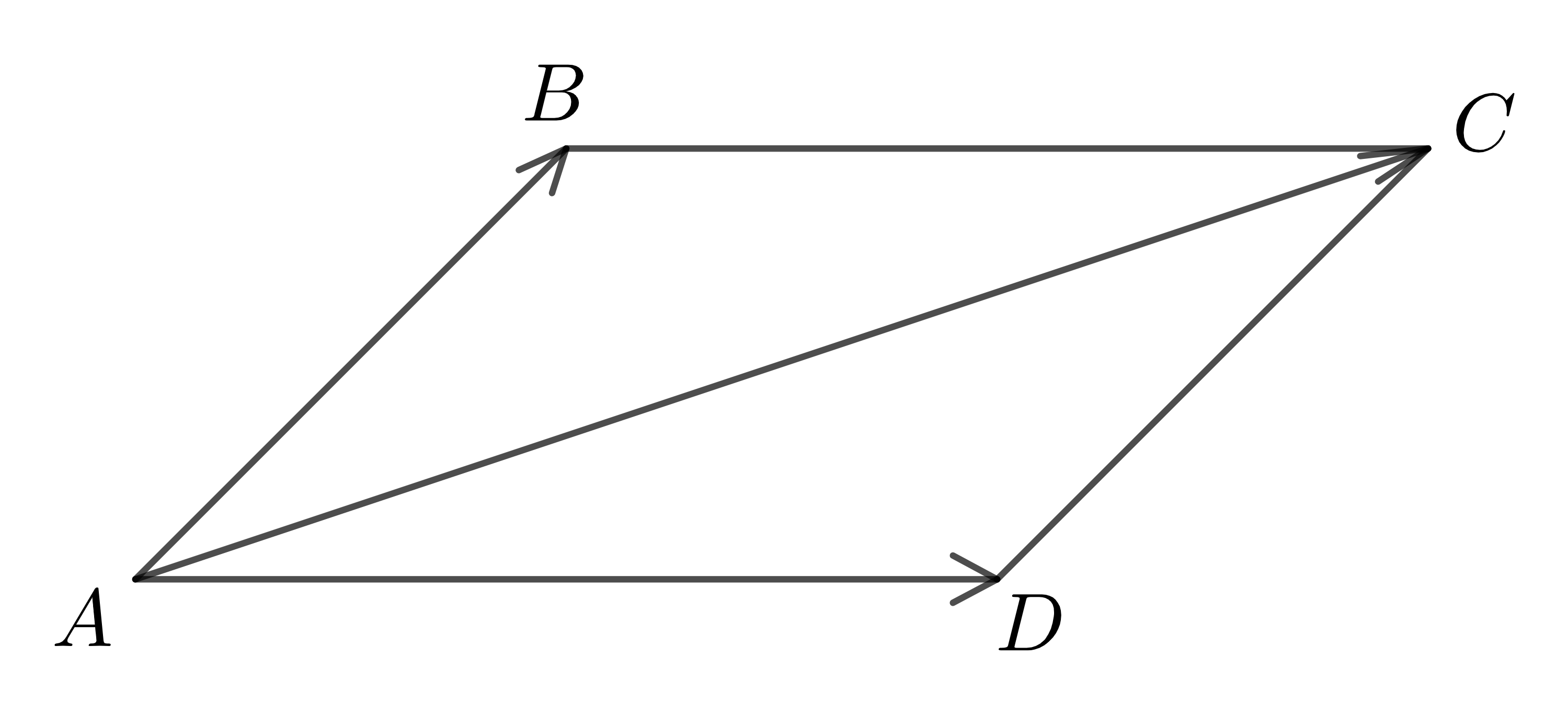
Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\).
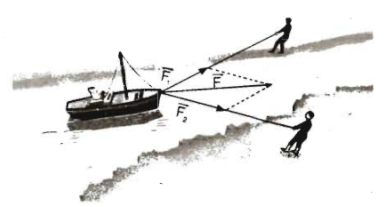
Ví dụ: Trong hình vẽ dưới đây, hai người đi dọc hai bên bờ kênh và cùng kéo một con thuyền với hai lực là \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\). Hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) tạo nên hợp lực \(\overrightarrow{F}\) là tổng của hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) làm con thuyền chuyển động. Đây chính là ứng dụng quy tắc hình bình hành trên.
Ví dụ 1: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB=6\), \(AC=8\). Tính độ dài của vectơ \(\overrightarrow{AB}+\overrightarrow{AC}\).
Giải:
Dựng hình chữ nhật \(ABDC\).

Theo tính chất của hình chữ nhật ta có \(AD=BC\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(ABC\) ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Suy ra \(AD=10\).
Áp dụng quy tắc hình bình hành trên ta có: \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
Do đó: \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=AD=10\).
Vậy độ dài vectơ \(\overrightarrow{AB}+\overrightarrow{AC}\) là 10 (đơn vị độ dài).
@1935025@
3. Tính chất của phép cộng các vectơ
Với ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) tuỳ ý ta có :
\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\) (tính chất giao hoán)
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)\) (tính chất kết hợp)
\(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}\) (tính chất của vectơ - không)
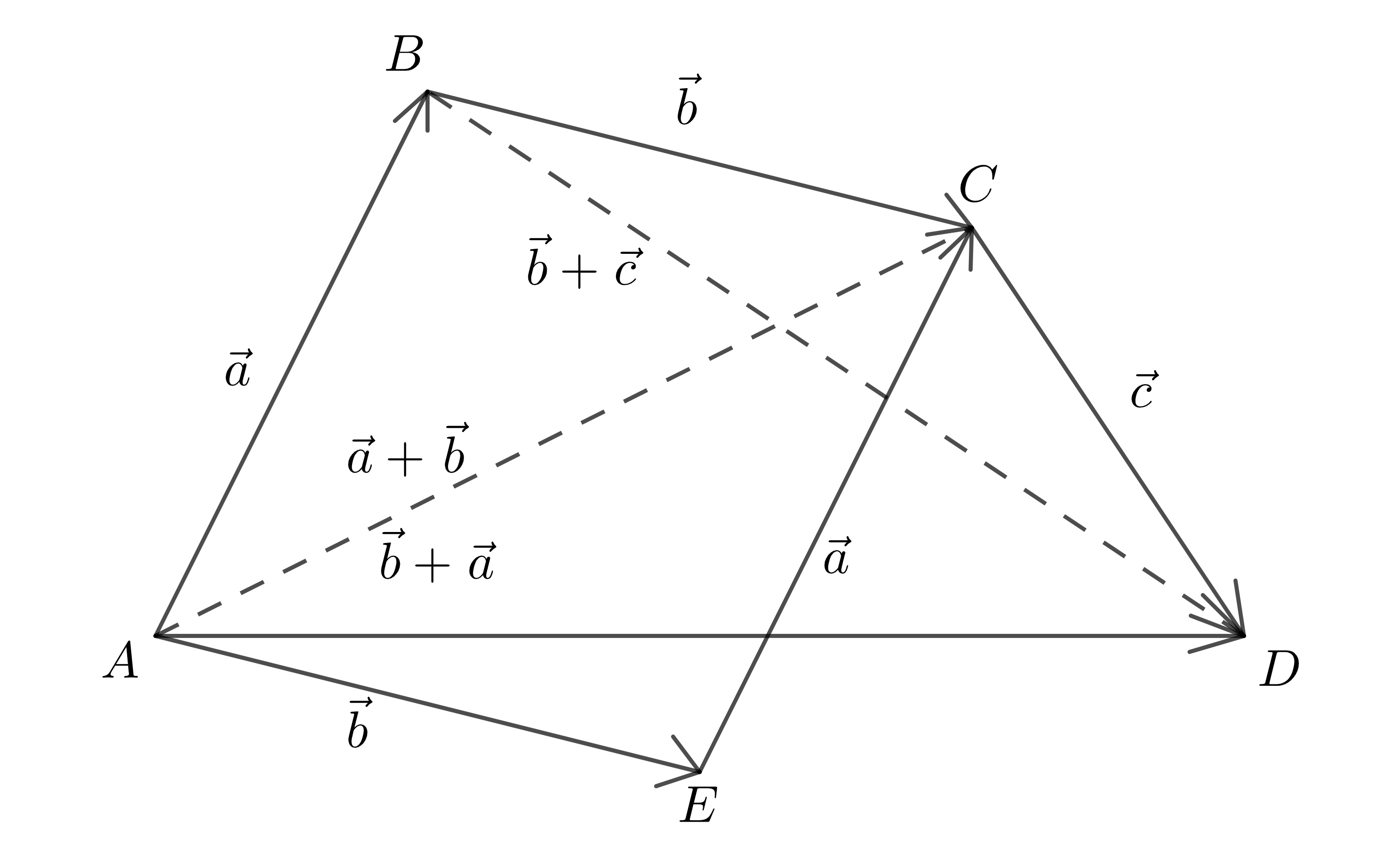
Các tính chất trên được minh hoạ bởi hình vẽ sau:
4. Hiệu của hai vectơ
a) Vectơ đối
Ví dụ: Trong hình bình hành \(ABCD\), vectơ \(\overrightarrow{AB}\) và vectơ \(\overrightarrow{CD}\) có cùng phương, ngược hướng với nhau và có độ dài bằng nhau. Ta nói vectơ \(\overrightarrow{CD}\) là vectơ đối của vectơ \(\overrightarrow{AB}\) .
Cho vectơ \(\overrightarrow{a}\). Vectơ có cùng độ dài và ngược hướng với \(\overrightarrow{a}\) được gọi là vectơ đối của vectơ \(\overrightarrow{a}\), kí hiệu là \(-\overrightarrow{a}\).
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của \(\overrightarrow{AB}\) là \(\overrightarrow{BA}\), nghĩa là \(-\overrightarrow{AB}=\overrightarrow{BA}\).
Đặc biệt, vectơ đối của vectơ \(\overrightarrow{0}\) là vectơ \(\overrightarrow{0}\).
Ví dụ: Xét tam giác \(ABC\) có \(D,E,F\) lần lượt là trung điểm của các cạnh \(BC,CA,AB\):
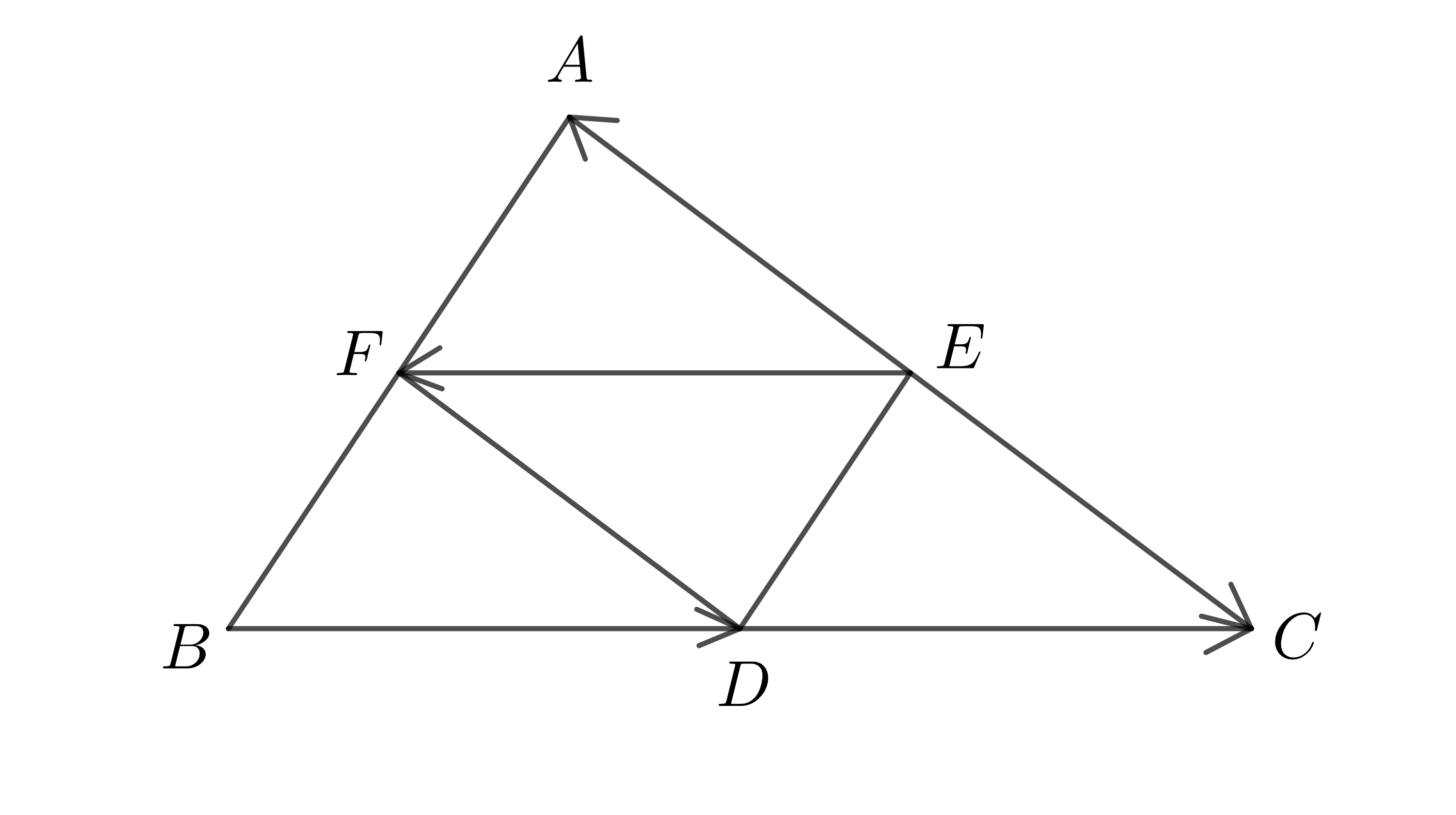
Khi đó ta có: \(\overrightarrow{EF}=-\overrightarrow{DC}\) ;
\(\overrightarrow{BD}=-\overrightarrow{EF}\) ;
\(\overrightarrow{EA}=-\overrightarrow{EC}\) ; ...
b) Định nghĩa hiệu của hai vectơ
Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Ta gọi hiệu của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là vectơ \(\overrightarrow{a}+\left(-\overrightarrow{b}\right)\), kí hiệu là \(\overrightarrow{a}-\overrightarrow{b}\).
Như vậy: \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+\left(-\overrightarrow{b}\right)\).
Từ định nghĩa hiệu của hai vectơ, ta suy ra:
Với ba điểm \(O,A,B\) tuỳ ý ta có \(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)

Chú ý: +) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.
+) Với ba điểm tuỳ ý \(A,B,C\) ta luôn có:
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) (quy tắc ba điểm)
\(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\) (quy tắc trừ)
Thực chất hai quy tắc trên được suy ra từ phép cộng vectơ.
Ví dụ 1. Chứng minh rằng với 4 điểm \(A,B,C,D\) bất kì ta luôn có \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\).
Giải:
Thật vậy, lấy một điểm \(O\) tuỳ ý ta luôn có:
\(\overrightarrow{AB}+\overrightarrow{CD}=\left(\overrightarrow{OB}-\overrightarrow{OA}\right)+\left(\overrightarrow{OD}-\overrightarrow{OC}\right)=\overrightarrow{OB}+\overrightarrow{OD}-\overrightarrow{OA}-\overrightarrow{OC}\)
\(\overrightarrow{AD}+\overrightarrow{CB}=\left(\overrightarrow{OD}-\overrightarrow{OA}\right)+\left(\overrightarrow{OB}-\overrightarrow{OC}\right)=\overrightarrow{OD}+\overrightarrow{OB}-\overrightarrow{OA}-\overrightarrow{OC}\)
Do đó \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\).
Ví dụ 2. Cho hình bình hành \(ABCD\) và một điểm \(M\) bất kì.
Chứng minh rằng \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\).
Giải:
Do \(ABCD\) là hình bình hành nên ta có \(\overrightarrow{AB}=\overrightarrow{DC}\).
Ta có: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\)
\(\Leftrightarrow\overrightarrow{MC}-\overrightarrow{MD}=\overrightarrow{MB}-\overrightarrow{MA}\) (thực hiện chuyển vế)
\(\Leftrightarrow\overrightarrow{DC}=\overrightarrow{AB}\) (quy tắc trừ) (luôn đúng)
Vậy \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\).
@1935653@
5. Áp dụng
a) Điểm \(I\) là trung điểm của đoạn thẳng \(AB\) khi và chỉ khi \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\) ;
b) Điểm \(G\) là trọng tâm của tam giác \(ABC\) khi và chỉ khi \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Chứng minh:
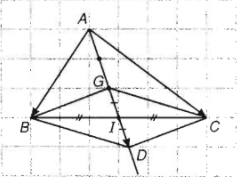
b) Trọng tâm \(G\) của tam giác \(ABC\) nằm trên trung tuyến \(AI\). Lấy \(D\) là điểm đối xứng với \(G\) qua \(I\). Khi đó \(BGCD\) là hình bình hành và \(G\) là trung điểm của đoạn thẳng \(AD\).
Suy ra \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (quy tắc hình bình hành) và \(\overrightarrow{GA}+\overrightarrow{GD}=\overrightarrow{0}\).
Khi đó ta có: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{GD}=\overrightarrow{0}\).
Ngược lại, giả sử \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\). Vẽ hình bình hành \(BGCD\) có \(I\) là giao điểm hai đường chéo. Khi đó \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\), suy ra \(\overrightarrow{GA}+\overrightarrow{GD}=\overrightarrow{0}\) nên \(G\) là trung điểm của đoạn thẳng \(AD\). Do đó 3 điểm \(A,G,I\) thẳng hàng, \(GA=2GI\) và điểm \(G\) nằm giữa \(A\) và \(I\).
Vậy \(G\) là trọng tâm của tam giác \(ABC\).
@1936566@