Bài 6: Ôn tập chương Đạo hàm

I. ĐỊNH NGHĨA ĐẠO HÀM

1. Định nghĩa đạo hàm tại một điểm

Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;b\right)\) và \(x_0\in\left(a;b\right)\). Nếu tồn tại giới hạn (hữu hạn)

               \(\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}\) 

thì giới hạn đó được gọi là đạo hàm của hàm số \(y=f\left(x\right)\) tại điểm \(x_0\) và kí hiệu là \(f'\left(x_0\right)\) (hoặc \(y'\left(x_0\right)\)) tức là 

                \(f'\left(x_0\right)=\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}\)   .

Chú ý: +) Đại lượng \(\Delta x=x-x_0\) được gọi là số gia của đối số tại \(x_0\)  ;

           +) Đại lượng \(\Delta y=f\left(x\right)-f\left(x_0\right)=f\left(x_0+\Delta x\right)-f\left(x_0\right)\) được gọi là số gia tương ứng của hàm số. Như vậy \(y'\left(x_0\right)=\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}\).

2. Cách tính đạo hàm bằng định nghĩa

Để tính đạo hàm của hàm số \(y=f\left(x\right)\) tại điểm \(x_0\) bằng định nghĩa, ta có quy tắc sau:

     Bước 1: Giả sử \(\Delta x\) là số gia của đối số tại \(x_0\) , tính

             \(\Delta y=f\left(x_0+\Delta x\right)-f\left(x_0\right)\)

     Bước 2: Lập tỉ số \(\dfrac{\Delta y}{\Delta x}\)

     Bước 3: Tìm \(\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}\).

3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lí 1: Nếu hàm số \(y=f\left(x\right)\) có đạo hàm tại \(x_0\) thì nó liên tục tại điểm đó.

Chú ý: 

a) Định lí trên tương đương với khẳng định: 

    Nếu hàm số \(y=f\left(x\right)\) gián đoạn tại \(x_0\) thì nó không có đạo hàm tại điểm đó.

b) Mệnh đề đảo của Định lí 1 không đúng.

   Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

4. Ý nghĩa hình học của đạo hàm

a) Tiếp tuyến của đường cong phẳng

Trên mặt phẳng toạ độ \(Oxy\) cho đường cong \(\left(C\right)\). Giả sử \(\left(C\right)\) là đường đồ thị của hàm số \(y=f\left(x\right)\) và \(M_0\left(x_0;f\left(x_0\right)\right)\in\left(C\right)\). Kí hiệu \(M\left(x;f\left(x\right)\right)\) là một điểm di chuyển trên \(\left(C\right)\). Đường thẳng \(M_0M\) là một cát tuyến của \(\left(C\right)\).

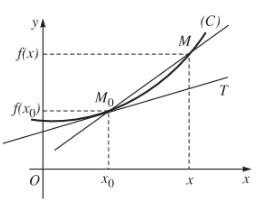
Nhận xét rằng khi \(x\rightarrow x_0\) thì \(M\left(x;f\left(x\right)\right)\) di chuyển trên \(\left(C\right)\) tới điểm \(M_0\left(x_0;f\left(x_0\right)\right)\) và ngược lại. Giả sử cát tuyến \(M_0M\) có vị trí giới hạn, kí hiệu là \(M_0T\) và \(M_0T\) được gọi là tiếp tuyến tại \(M_0\) của \(\left(C\right)\). Điểm \(M_0\) được gọi là tiếp điểm.

b) Ý nghĩa hình học của đạo hàm

Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;b\right)\) và có đạo hàm tại \(x_0\in\left(a;b\right)\). Gọi \(\left(C\right)\) là đồ thị của hàm số đó.

Đạo hàm của hàm số \(y=f\left(x\right)\) tại điểm \(x_0\) là hệ số góc của tiếp tuyến \(M_0T\) của \(\left(C\right)\) tại điểm \(M_0\left(x_0;f\left(x_0\right)\right)\).

c) Phương trình tiếp tuyến

Phương trình tiếp tuyến của đồ thị \(\left(C\right)\) của hàm số \(y=f\left(x\right)\) tại điểm \(M_0\left(x_0;f\left(x_0\right)\right)\) là

           \(y-y_0=f'\left(x_0\right)\left(x-x_0\right)\)

trong đó \(y_0=f\left(x_0\right)\).

5. Ý nghĩa vật lí của đạo hàm

a) Vận tốc tức thời

Xét chuyển động thẳng xác định bởi phương trình \(s=s\left(t\right)\), với \(s=s\left(t\right)\) là một hàm số có đạo hàm. Vận tốc tức thời của chuyển động tại thời điểm \(t_0\) là đạo hàm của hàm số \(s=s\left(t\right)\) tại \(t_0\): 

         \(v\left(t_0\right)=s'\left(t_0\right)\).

b) Cường độ tức thời

Nếu điện lượng \(Q\) truyền trong dây dẫn là một hàm số của thời gian: \(Q=Q\left(t\right)\) (\(Q=Q\left(t\right)\) là một hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm \(t_0\) là đạo hàm của hàm số \(Q=Q\left(t\right)\) tại \(t_0\):

         \(I\left(t_0\right)=Q'\left(t_0\right)\).

6. Đạo hàm trên một khoảng

Hàm số \(y=f\left(x\right)\) được gọi là có đạo hàm trên khoảng \(\left(a;b\right)\) nếu nó có đạo hàm tại mọi điểm \(x\) trên khoảng đó.

Khi đó, ta gọi hàm số \(f'\): \(\left(a;b\right)\rightarrow R\)

                                              \(x\rightarrow f'\left(x\right)\)

là đạo hàm của hàm số \(y=f\left(x\right)\) trên khoảng \(\left(a;b\right)\) , kí hiệu là \(y'\) hay \(f'\left(x\right)\).

II. QUY TẮC TÍNH ĐẠO HÀM

1. Quy tắc tính đạo hàm của các hàm số thường gặp

- Hàm số \(y=x^n\) (\(n\in N,n>1\)) có đạo hàm tại mọi \(x\in R\) và 

               \(\left(x^n\right)'=nx^{n-1}\).

Ví dụ: \(\left(x^2\right)'=2x\) 

Nhận xét: +) Đạo hàm của hàm hằng bằng 0 :  \(\left(c\right)'=0\)

                 +) Đạo hàm của hàm số \(y=x\) bằng 1 :  \(\left(x\right)'=1\)

- Hàm số \(y=\sqrt{x}\) có đạo hàm tại mọi \(x\) dương và

                \(\left(\sqrt{x}\right)'=\dfrac{1}{2\sqrt{x}}\).

- Giả sử \(u=u\left(x\right)\), \(v=v\left(x\right)\) là các hàm số có đạo hàm tại điểm \(x\) thuộc khoảng xác định. Ta có:

               \(\left(u+v\right)'=u'+v'\)

               \(\left(u-v\right)'=u'-v'\)

               \(\left(uv\right)'=u'v+uv'\)

               \(\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}\left(v=v\left(x\right)\ne0\right)\).

- Hệ quả 1: Nếu \(k\) là một hằng số thì \(\left(ku\right)'=ku'\).

- Hệ quả 2:\(\left(\dfrac{1}{v}\right)'=-\dfrac{v'}{v^2}\left(v=v\left(x\right)\ne0\right)\).

2. Đạo hàm của hàm hợp

Giả sử \(u=g\left(x\right)\) là hàm số của \(x\), xác định trên khoảng \(\left(a;b\right)\) và lấy giá trị trên khoảng \(\left(c;d\right)\); \(y=f\left(u\right)\) là hàm số của \(u\), xác định trên \(\left(c;d\right)\) và lấy giá trị trên \(R\). Khi đó ta lập một hàm số xác định trên \(\left(a;b\right)\) và lấy giá trị trên \(R\) theo quy tắc:

                        \(x\rightarrow f\left(g\left(x\right)\right)\)

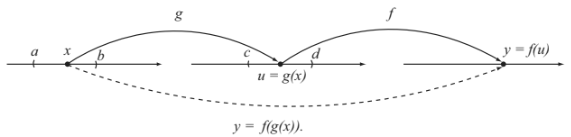
Ta gọi hàm số \(y=f\left(g\left(x\right)\right)\) là hàm hợp của hàm số \(y=f\left(u\right)\) và \(u=g\left(x\right)\).

- Quy tắc tính đạo hàm của hàm hợp:

Nếu hàm số \(u=g\left(x\right)\) các đạo hàm tại \(x\) là \(u'_x\) và hàm số \(y=f\left(u\right)\) có đạo hàm tại \(u\) là \(y'_u\) thì hàm hợp \(y=f\left(g\left(x\right)\right)\) có đạo hàm tại \(x\) là

                \(y'_x=y'_u.u'_x\)

III. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC

1. Đạo hàm của hàm số \(y=\sin x\)

Hàm số \(y=\sin x\) có đạo hàm tại mọi \(x\in R\) và

           \(\left(\sin x\right)'=\cos x\).

Nếu \(y=\sin u\) và \(u=u\left(x\right)\) thì 

           \(\left(\sin u\right)'=u'.\cos u\)

2. Đạo hàm của hàm số \(y=\cos x\)

Hàm số \(y=\cos x\) có đạo hàm tại mọi \(x\in R\) và 

           \(\left(\cos x\right)'=-\sin x\).

Nếu \(y=\cos u\) và \(u=u\left(x\right)\) thì 

           \(\left(\cos u\right)'=-u'.\sin u\)

3. Đạo hàm của hàm số \(y=\tan x\)

Hàm số \(y=\tan x\) có đạo hàm tại mọi \(x\ne\dfrac{\pi}{2}+k\pi,k\in Z\) và

           \(\left(\tan x\right)'=\dfrac{1}{\cos^2x}\).

Nếu \(y=\tan u\) và \(u=u\left(x\right)\) thì

           \(\left(\tan u\right)'=\dfrac{u'}{\cos^2u}\)

4. Đạo hàm của hàm số \(y=\cot x\)

Hàm số \(y=\cot x\) có đạo hàm tại mọi \(x\ne k\pi,k\in Z\) và

         \(\left(\cot x\right)'=-\dfrac{1}{\sin^2x}\).

Nếu \(y=\cot u\) và \(u=u\left(x\right)\) thì

          \(\left(\cot u\right)'=-\dfrac{u'}{\sin^2u}\).

IV. VI PHÂN

1. Định nghĩa vi phân

Cho hàm số \(y=f\left(x\right)\), xác định trên khoảng \(\left(a;b\right)\) và có đạo hàm tại điểm \(x_0\in\left(a;b\right)\). Giả sử \(\Delta x\) là số gia của \(x\).

Ta gọi tích \(f'\left(x\right)\Delta x\) là vi phân của hàm số  \(y=f\left(x\right)\) tại \(x\) ứng với số gia \(\Delta x\), ký hiệu \(dy\) hoặc \(df\left(x\right)\), tức là

             \(dy=df\left(x\right)=f'\left(x\right)\Delta x\).

Chú ý: Áp dụng định nghĩa trên vào hàm số \(y=x\) ta có

                      \(dx=d\left(x\right)=\left(x\right)'\Delta x=1.\Delta x=\Delta x\)

            Do đó với hàm số \(y=f\left(x\right)\) ta có

                      \(dy=df\left(x\right)=f'\left(x\right)dx\)

2. Ứng dụng vi phân tính gần đúng

Theo định nghĩa đạo hàm ta có:

               \(f'\left(x_0\right)=\lim\limits_{x\rightarrow x_0}\dfrac{\Delta y}{\Delta x}\) 

Do đó với \(\left|\Delta x\right|\) đủ nhỏ thì 

               \(\dfrac{\Delta y}{\Delta x}\approx f'\left(x_0\right)\) hay \(\Delta y\approx f'\left(x_0\right)\Delta x\)

Từ đó ta có \(f\left(x_0+\Delta x\right)-f\left(x_0\right)\approx f'\left(x_0\right)\Delta x\)

hay \(f\left(x_0+\Delta x\right)\approx f\left(x_0\right)+f'\left(x_0\right)\Delta x\)

Đó là công thức tính gần đúng đơn giản nhất.

Ví dụ: Tính giá trị gần đúng của \(\sqrt{3,99}\).

Giải:

Đặt \(f\left(x\right)=\sqrt{x}\) , ta có \(f'\left(x\right)=\dfrac{1}{2\sqrt{x}}\)

Theo công thức tính gần đúng, với \(x_0=4,\Delta x=-0,01\) ta có

      \(f\left(3,99\right)=f\left(4-0,01\right)\approx f\left(4\right)+f'\left(4\right)\left(-0,01\right)\)

tức là \(\sqrt{3,99}=\sqrt{4-0,01}\approx\sqrt{4}+\dfrac{1}{2\sqrt{x}}\left(-0,01\right)=1,9975\).

V. ĐẠO HÀM CẤP HAI

1. Định nghĩa

Giả sử hàm số \(y=f\left(x\right)\) có đạo hàm tại mỗi điểm \(x\in\left(a;b\right)\). Khi đó hệ thức \(y'=f'\left(x\right)\) xác định một hàm số mới trên khoảng \(\left(a;b\right)\). Nếu hàm số \(y'=f'\left(x\right)\) lại có đạo hàm tại \(x\) thì ta gọi đạo hàm của \(y'\) là đạo hàm cấp hai của hàm số \(y=f\left(x\right)\) tại \(x\) và kí hiệu là \(y''\) hay \(f''\left(x\right)\)

Chú ý:

     +) Đạo hàm cấp 3 của hàm số \(y=f\left(x\right)\) được định nghĩa tương tự và kí hiệu là \(y'''\) hoặc \(f'''\left(x\right)\) hoặc \(f^{\left(3\right)}\left(x\right)\)  ;

     +) Cho hàm số \(y=f\left(x\right)\) có đạo hàm cấp \(n-1\), kí hiệu là \(f^{\left(n-1\right)}\left(x\right)\) \(\left(n\in N,n\ge4\right)\). Nếu \(f^{\left(n-1\right)}\left(x\right)\) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp \(n\) của \(f\left(x\right)\), kí hiệu là \(y^{\left(n\right)}\) hoặc \(f^{\left(n\right)}\left(x\right)\).

         \(f^{\left(n\right)}\left(x\right)=\left(f^{\left(n-1\right)}\left(x\right)\right)'\).

2. Ý nghĩa cơ học của đạo hàm cấp hai

Xét chuyển động xác định bởi phương trình \(s=f\left(t\right)\), trong đó \(s=f\left(t\right)\) là một hàm số có đạo hàm đến cấp hai. Vận tốc tức thời tại \(t\) của chuyển động là \(v\left(t\right)=f'\left(t\right)\).

Lấy số gia \(\Delta t\) tại \(t\) thì \(v\left(t\right)\) có số gia tương ứng là \(\Delta v\).

Tỉ số \(\dfrac{\Delta v}{\Delta t}\) được gọi là gia tốc trung bình của chuyển động trong khoảng thời gian \(\Delta t\). Nếu tồn tại

               \(v'\left(t\right)=\lim\limits_{\Delta t\rightarrow0}\dfrac{\Delta v}{\Delta t}=\gamma\left(t\right)\) 

ta gọi \(v'\left(t\right)=\gamma\left(t\right)\) là gia tốc tức thời của chuyển động tại thời điểm \(t\).

Vì \(v\left(t\right)=f'\left(t\right)\) nên 

              \(\gamma\left(t\right)=f''\left(x\right)\).

a) Ý nghĩa cơ học:

Đạo hàm cấp hai \(f''\left(t\right)\) là gia tốc tức thời của chuyển động \(s=f\left(t\right)\) tại thời điểm \(t\).

b) Ví dụ:

Xét chuyển động có phương trình 

          \(s\left(t\right)=A\sin\left(\omega t+\varphi\right)\)  (\(A,\omega,\varphi\) là các hằng số).

Tìm gia tốc tức thời tại thời điểm \(t\) của chuyển động.

Giải:

Gọi \(v\left(t\right)\) là vận tốc tức thời của chuyển động tại thời điểm \(t\), ta có:

       \(v\left(t\right)=s'\left(t\right)=\left[A\sin\left(\omega t+\varphi\right)\right]'=A\omega\cos\left(\omega t+\varphi\right)\)

Vậy gia tốc tức thời của chuyển động tại thời điểm \(t\) là

       \(\gamma\left(t\right)=s''\left(t\right)=v'\left(t\right)=-A\omega^2\sin\left(\omega t+\varphi\right)\).