Ôn tập chương III
Nội dung lý thuyết
Các phiên bản khácI. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1. Vectơ chỉ phương của đường thẳng
Định nghĩa: Vectơ \(\overrightarrow{u}\) được gọi là vectơ chỉ phương của đường thẳng \(\Delta\) nếu \(\overrightarrow{u}\ne\overrightarrow{0}\) và giá của \(\overrightarrow{u}\) song song hoặc trùng với \(\Delta\).
Nhận xét:
- Nếu \(\overrightarrow{u}\) là một vectơ chỉ phương của đường thẳng \(\Delta\) thì \(k\overrightarrow{u}\left(k\ne0\right)\) cũng là một vectơ chỉ phương của \(\Delta\). Do đó một đường thẳng có vô số vectơ chỉ phương.
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó.
2. Phương trình tham số của đường thẳng
- Định nghĩa:
Trong mặt phẳng \(Oxy\) cho đường thẳng \(\Delta\) đi qua điểm \(M_0\left(x_0;y_0\right)\) và nhận \(\overrightarrow{u}=\left(u_1;u_2\right)\) làm vectơ chỉ phương. Với mỗi điểm \(M\left(x;y\right)\) bất kì trong mặt phẳng, ta có \(\overrightarrow{M_oM}=\left(x-x_0;y-y_0\right)\). Khi đó: \(M\in\Delta\Leftrightarrow\) \(\overrightarrow{M_0M}\) cùng phương với \(\overrightarrow{u}\) \(\Leftrightarrow\overrightarrow{M_0M}=t\overrightarrow{u}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-x_0=tu_1\\y-y_0=tu_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=x_0+tu_1\\y=y_0+tu_2\end{matrix}\right.\) (1)
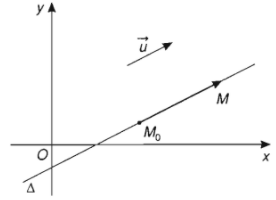
Hệ phương trình (1) được gọi là phương trình tham số của đường thẳng \(\Delta\), trong đó \(t\) là tham số.
Cho \(t\) một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng \(\Delta\).
Ví dụ: Một đường thẳng \(d\) có phương trình tham số là \(\left\{{}\begin{matrix}x=5-6t\\y=2+8t\end{matrix}\right.\).
Ta có thể xác định một vectơ chỉ phương của đường thẳng \(d\) là \(\overrightarrow{u}=\left(-6;8\right)\)
Cho \(t=1\) ta xác định được một điểm nằm trên \(d\) có toạ độ là \(A\left(-1;10\right)\).
- Liên hệ giữa vectơ chỉ phương và hệ số góc của đường thẳng:
Cho đường thẳng \(\Delta\) có phương trình tham số \(\left\{{}\begin{matrix}x=x_0+tu_1\\y=y_0+tu_2\end{matrix}\right.\)
Nếu \(u_1\ne0\) thì từ phương trình tham số của \(\Delta\) ta có \(\left\{{}\begin{matrix}t=\dfrac{x-x_0}{u_1}\\y-y_0=tu_2\end{matrix}\right.\)
Suy ra \(y-y_0=\dfrac{u_2}{u_1}\left(x-x_0\right)\)
Đặt \(k=\dfrac{u_2}{u_1}\) ta được \(y-y_0=k\left(x-x_0\right)\)
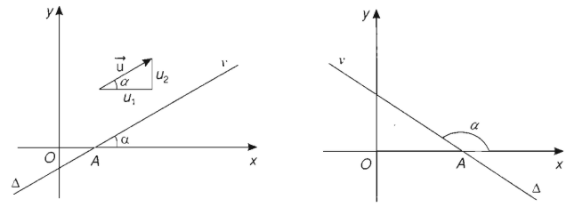
Gọi \(A\) là giao điểm của \(\Delta\) với trục hoành. \(Av\) là tia thuộc \(\Delta\) ở về phía mặt phẳng tạ độ phía trên (chứa tia \(Oy\)). Đặt \(\alpha=\widehat{xAv}\), ta thấy \(k=\tan\alpha\).
Số \(k\) chính là hệ số góc của đường thẳng \(\Delta\).
Như vậy, Nếu đường thẳng \(\Delta\) có vectơchỉ phương \(\overrightarrow{u}=\left(u_1;u_2\right)\) với \(u_1\ne0\) thì \(\Delta\) có hệ số góc \(k=\dfrac{u_2}{u_1}\).
3. Vectơ pháp tuyến của đường thẳng
Định nghĩa: Vectơ \(\overrightarrow{n}\) được gọi là vectơ pháp tuyến của đường thẳng \(\Delta\) nếu \(\overrightarrow{n}\ne\overrightarrow{0}\) và \(\overrightarrow{n}\) vuông góc với vectơ chỉ phương của \(\Delta\).
Ví dụ: Đường thẳng \(\Delta\) có phương trình \(\left\{{}\begin{matrix}x=-5+2t\\y=4+3t\end{matrix}\right.\) và vectơ \(\overrightarrow{n}=\left(3;-2\right)\).
Vectơ chỉ phương của \(\Delta\) là \(\overrightarrow{u}=\left(2;3\right)\)
Ta có \(\cos\left(\overrightarrow{u},\overrightarrow{n}\right)=\dfrac{2.3+3.\left(-2\right)}{\sqrt{2^2+3^2}.\sqrt{3^2+\left(-2\right)^2}}=0\) suy ra \(\left(\overrightarrow{u},\overrightarrow{n}\right)=90^0\)
Hay vectơ \(\overrightarrow{n}=\left(3;-2\right)\) vuông góc với \(\overrightarrow{u}\)
Ta nói \(\overrightarrow{n}=\left(3;-2\right)\) là vectơ pháp tuyến của \(\Delta\).
Nhận xét:
- Nếu \(\overrightarrow{n}\) là một vectơ pháp tuyến của của đường thẳng \(\Delta\) thì \(k\overrightarrow{n}\left(k\ne0\right)\) cũng là một vectơ pháp tuyến của \(\Delta\). Do đó một đường thẳng có vô số vectơ pháp tuyến.
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ pháp tuyến của nó.
4. Phương trình tổng quát của đường thẳng
- Định nghĩa: Phương trình \(ax+by+c=0\) với \(a\) và \(b\) không đồng thời bằng \(0\), được gọi là phương trình tổng quát của đường thẳng.
Nhận xét: Nếu đường thẳng \(\Delta\) có phương trình là \(ax+by+c=0\) thì \(\Delta\) có vectơ pháp tuyến là \(\overrightarrow{n}=\left(a;b\right)\) và vectơ chỉ phương là \(\overrightarrow{u}=\left(-b;a\right)\).
Ví dụ: Lập phương trình tổng quát của đường thẳng \(\Delta\) đi qua hai điểm \(A\left(2;2\right)\) và \(B\left(4;3\right)\)
Giải:
Đường thẳng \(\Delta\) đi qua hai điểm \(A\left(2;2\right)\) và \(B\left(4;3\right)\) nên \(\Delta\) có vectơ chỉ phương là \(\overrightarrow{AB}=\left(2;1\right)\).
Từ đó suy ra \(\Delta\) có vectơ pháp tuyến là \(\overrightarrow{n}=\left(-1;2\right)\).
Vậy \(\Delta\) có phương trình tổng quát là \(\left(-1\right).\left(x-2\right)+2.\left(y-2\right)=0\)
Hay \(x-2y+2=0\).
- Các trường hợp đặc biệt:
Cho đường thẳng \(\Delta\) có phương trình tổng quát \(ax+by+c=0\) (1)
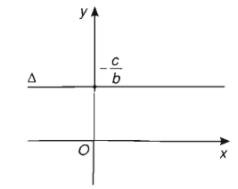
+) Nếu \(a=0\) phương trình (1) trở thành \(by+c=0\) hay \(y=-\dfrac{c}{b}\)
Khi đó đường thẳng \(\Delta\) vuông góc với trục \(Oy\) tại điểm \(\left(0;-\dfrac{c}{b}\right)\)
+) Nếu \(b=0\) thì phương trình (1) trở thành \(ax+c=0\) hay \(x=-\dfrac{c}{a}\)
Khi đó đường thẳng \(\Delta\) vuông góc với trục \(Ox\) tại điểm \(\left(-\dfrac{c}{a};0\right)\)

+) Nếu \(c=0\) thì phương trình (1) trở thành \(ax+by=0\)
Khi đó đường thẳng \(\Delta\) đi qua gốc toạ độ \(O\)

+) Nếu \(a,b,c\) đều khác 0 ta có thể đưa phương trình (1) về dạng \(\dfrac{x}{a_0}+\dfrac{y}{b_0}=1\) (2)
với \(a_0=-\dfrac{c}{a}\), \(b_0=-\dfrac{c}{b}\).
Phương trình (2) được gọi là phương trình đường thẳng theo đoạn chắn , đường thẳng này cắt \(Ox\) và \(Oy\) lần lượt tại \(M\left(a_0;0\right)\) và \(N\left(0;b_0\right)\).

5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng \(\Delta_1\) và \(\Delta_2\) có phương trình tổng quát lần lượt là
\(a_1x+b_1y+c_1=0\) và \(a_2x+b_2y+c_2=0\)
Toạ độ giao điểm của \(\Delta_1\) và \(\Delta_2\) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0\end{matrix}\right.\) (I)
Ta có các trường hợp:
a) Hệ (I) có một nghiệm \(\left(x_0;y_0\right)\). Khi đó \(\Delta_1\) cắt \(\Delta_2\) tại điểm \(M_0\left(x_0;y_0\right)\).
b) Hệ (I) có vô số nghiệm. Khi đó \(\Delta_1\) trùng với \(\Delta_2\).
c) Hệ (I) vô nghiệm. Khi đó \(\Delta_1\) và \(\Delta_2\) không có điểm chung, hay \(\Delta_1\) song song với \(\Delta_2\).
6. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng \(\Delta_1\) và \(\Delta_2\) được kí hiệu là \(\widehat{\left(\Delta_1,\Delta_2\right)}\) hoặc \(\left(\Delta_1,\Delta_2\right)\).
Cho hai đường thẳng:
\(\Delta_1\): \(a_1x+b_1y+c_1=0\)
\(\Delta_2\): \(a_2x+b_2y+c_2=0\)
Đặt \(\varphi=\left(\Delta_1;\Delta_2\right)\) thì ta thấy \(\varphi\) bằng hoặc bù với góc giữa \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) là hai vectơ pháp tuyến của \(\Delta_1\) và \(\Delta_2\). Vì \(\cos\varphi\ge0\) nên ta suy ra
\(\cos\varphi=\left|\cos\left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\dfrac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|}\)
Vậy
\(\cos\varphi=\dfrac{\left|a_1a_2+b_1b_2\right|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}\)
- Chú ý: +) \(\Delta_1\perp\Delta_2\Leftrightarrow\overrightarrow{n_1}\perp\overrightarrow{n_2}\Leftrightarrow a_1a_2+b_1b_2=0\)
+) Nếu \(\Delta_1\) và \(\Delta_2\) có phương trình \(y=k_1x+m_1\) và \(y=k_2x+m_2\) thì
\(\Delta_1\perp\Delta_2\Leftrightarrow k_1.k_2=-1\)
7. Công thức tính khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng \(Oxy\) cho đường thẳng \(\Delta\) có phương trình \(ax+by+c=0\) và điểm \(M_0\left(x_0;y_0\right)\). Khoảng cách từ điểm \(M_0\) đến đường thẳng \(\Delta\), kí hiệu là \(d\left(M_0,\Delta\right)\), được tính bởi công thức:
\(d\left(M_0,\Delta\right)=\dfrac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}\)
@36750@
II. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
1. Phương trình đường tròn có tâm và bán kính cho trước
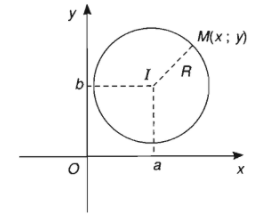
Trong mặt phẳng \(Oxy\) cho đường thẳng \(\left(C\right)\) tâm \(I\left(a;b\right)\), bán kính \(R\).
Phương trình \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) được gọi là phương trình đường tròn tâm \(I\left(a;b\right)\) bán kính \(R\).
Chẳng hạn, phương trình đường tròn tâm \(I\left(2;-3\right)\) bán kính \(R=5\) là: \(\left(x-2\right)^2+\left(y+3\right)^2=25\)
2. Nhận xét
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) có thể được viết dưới dạng \(x^2+y^2-2ax-2by+c=0\) , trong đó \(c=a^2+b^2-R^2\).
Ngược lại, phương trình \(x^2+y^2-2ax-2by+c=0\) là phương trình của đường tròn \(\left(C\right)\) khi và chỉ khi \(a^2+b^2-c>0\). Khi đó đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\) và bán kính \(R=\sqrt{a^2+b^2-c}\).
3. Phương trình tiếp tuyến của đường tròn
Cho điểm \(M_0\left(x_0;y_0\right)\) nằm trên đường tròn \(\left(C\right)\) tâm \(I\left(a;b\right)\).
Gọi \(\Delta\) là tiếp tuyến với \(\left(C\right)\) tại \(M_0\).
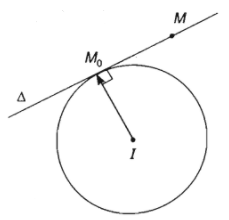
Ta có \(M_0\) thuộc \(\Delta\) và vectơ \(\overrightarrow{IM_0}=\left(x_0-a;y_0-b\right)\) là vectơ pháp tuyến của \(\Delta\).
Do đó \(\Delta\) có phương trình là:
\(\left(x_0-a\right)\left(x-x_0\right)+\left(y_0-b\right)\left(y-y_0\right)=0\) (2)
Phương trình (2) là phương trình tiếp tuyến của đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) tại điểm \(M_0\) nằm trên đường tròn.
Ví dụ: Viết phương trình tiếp tuyến tại điểm \(M\left(3;4\right)\) thuộc đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-2\right)^2=8\).
Giải:
Từ phương trình \(\left(x-1\right)^2+\left(y-2\right)^2=8\) ta suy ra \(\left(C\right)\) có tâm \(I\left(1;2\right)\)
Suy ra phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là
\(\left(3-1\right)\left(x-3\right)+\left(4-2\right)\left(y-4\right)=0\)
\(\Leftrightarrow2x+2y-14=0\)
\(\Leftrightarrow x+y-7=0\)
Vậy phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là \(x+y-7=0\).
@1998849@
III. PHƯƠNG TRÌNH ELIP
1. Định nghĩa đường elip
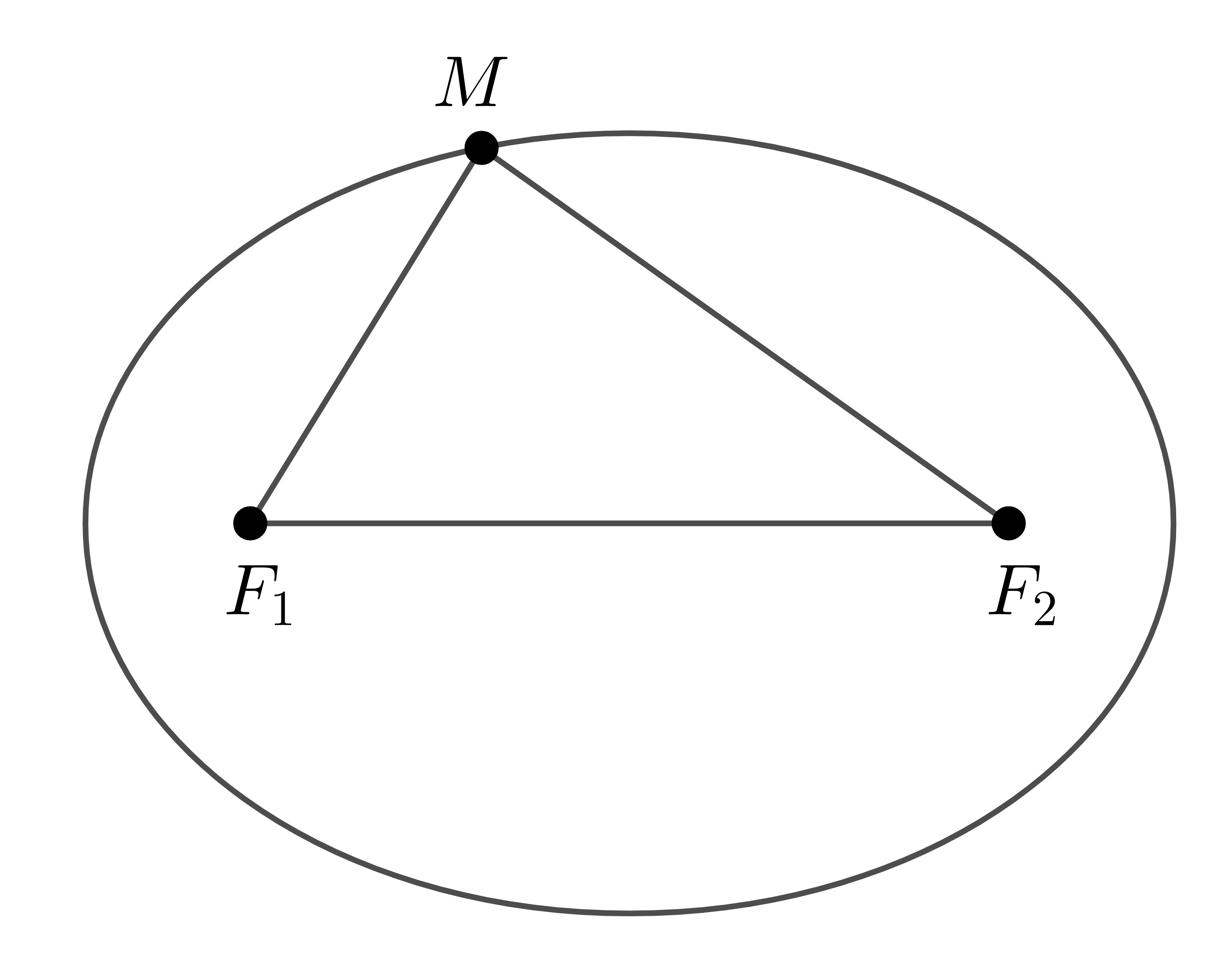
Định nghĩa: Cho hai điểm cố định \(F_1,F_2\) và một độ dài không đổi \(2a\) lớn hơn \(F_1F_2\). Elip là tập hợp các điểm \(M\) trong mặt phẳng sao cho
\(F_1M+F_2M=2a\)
Các điểm \(F_1\) và \(F_2\) gọi là các tiêu điểm của elip. Độ dài \(F_1F_2=2c\) gọi là tiêu cự của elip.
2. Phương trình chính tắc của elip
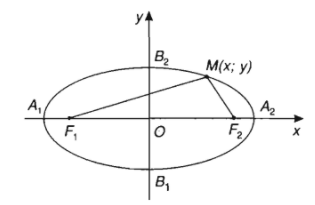
Cho elip \(\left(E\right)\) có các tiêu điểm \(F_1\) và \(F_2\). Điểm \(M\) thuộc elip khi và chỉ khi \(F_1M+F_2M=2a\). Chọn hệ trục toạ độ \(Oxy\) sao cho \(F_1=\left(-c;0\right)\), \(F_2=\left(c;0\right)\).
Khi đó người ta chứng minh được:
\(M\left(x;y\right)\in\left(E\right)\Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) (1)
trong đó \(b^2=a^2-c^2\).
Phương trình (1) gọi là phương trình chính tắc của elip.
3. Hình dạng của elip

Xét elip \(\left(E\right)\) có phương trình (1):
a) Nếu điểm \(M\left(x;y\right)\) thuộc \(\left(E\right)\) thì các điểm \(M_1\left(-x;y\right)\), \(M_2\left(x;-y\right)\) và \(M_3\left(-x;-y\right)\) cũng thuộc \(\left(E\right)\).
Vậy \(\left(E\right)\) có các trục đối xứng là \(Ox,Oy\) và có tâm đối xứng là gốc \(O\).
b) Thay \(y=0\) vào (1) ta có \(x=\pm a\), suy ra \(\left(E\right)\) cắt \(Ox\) tại hai điểm \(A_1\left(-a;0\right)\) và \(A_2\left(a;0\right)\). Tương tự thay \(x=0\) vào (1) ta được \(y=\pm b\), vậy \(\left(E\right)\) cắt \(Oy\) tại hai điểm \(B_1\left(0;-b\right)\) và \(B_2\left(0;b\right)\).
Các điểm \(A_1,A_2,B_1,B_2\) gọi là các đỉnh của elip.
Đoạn thẳng \(A_1A_2\) gọi là trục lớn, đoạn thẳng \(B_1B_2\) gọi là trục nhỏ của elip.
Ví dụ: Elip \(\left(E_1\right)\): \(\dfrac{x^2}{9}+\dfrac{y^2}{1}=1\) có:
+) Các đỉnh là \(A_1\left(-3;0\right)\), \(A_2\left(3;0\right)\), \(B_1\left(0;-1\right)\), \(B_2\left(0;1\right)\)
+) \(A_1A_2=6\) là trục lớn, \(B_1B_2=2\) là trục nhỏ.
4. Liên hệ giữa đường tròn và đường elip
a) Từ hệ thức \(b^2=a^2-c^2\) ta thấy nếu tiêu cự của elip càng nhỏ thì \(b\) càng gần \(a\), tức là trục nhỏ của elip càng gần bằng trục lớn. Lúc đó elip có dạng gần như đường tròn.
b) Trong mặt phẳng \(Oxy\) cho đường tròn \(\left(C\right)\) có phương trình \(x^2+y^2=a^2\)
Với mỗi điểm \(M\left(x;y\right)\) thuộc đường tròn ta xét điểm \(M'\left(x';y'\right)\) sao cho
\(\left\{{}\begin{matrix}x'=x\\y'=\dfrac{b}{a}y\end{matrix}\right.\) (với \(0< b< a\))
thì tập hợp các điểm \(M'\) có toạ độ thoả mãn phương trình \(\dfrac{x'^2}{a^2}+\dfrac{y'^2}{b^2}=1\) là một elip \(\left(E\right)\).
Khi đó ta nói đường tròn \(\left(C\right)\) được co thành elip \(\left(E\right)\).

@1999368@