Bài 4: Ôn tập chương Hàm số lượng giác và phương trình lượng giác
Nội dung lý thuyết
Các phiên bản khácI. HÀM SỐ LƯỢNG GIÁC
1. Định nghĩa
Bảng giá trị lượng giác của các cung đặc biệt
Cung Giá trị lượng giác | 0 | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) |
| \(\sin x\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | 1 |
| \(\cos x\) | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | 0 |
| \(\tan x\) | 0 | \(\dfrac{\sqrt{3}}{3}\) | 1 | \(\sqrt{3}\) | || |
| \(\cot x\) | || | \(\sqrt{3}\) | 1 | \(\dfrac{\sqrt{3}}{3}\) | 0 |
a) Hàm số sin
Quy tắc đặt tương ứng mỗi số thực \(x\) với số thực \(\sin x\):
\(\sin\) : \(R\rightarrow R\)
\(x\rightarrow y=\sin x\)
được gọi là hàm số sin, kí hiệu là \(y=\sin x\).
Tập xác định của hàm số \(\sin\) là \(R\).
b) Hàm số côsin
Quy tắc đặt tương ứng mỗi số thực \(x\) với số thực \(\cos x\):
\(\cos\) : \(R\rightarrow R\)
\(x\rightarrow y=\cos x\)
được gọi là hàm số côsin , kí hiệu là \(y=\cos x\).
Tập xác định của hàm số côsin là \(R\).
c) Hàm số tang
Hàm số tang là hàm số được xác định bởi công thức :
\(y=\dfrac{\sin x}{\cos x},\left(\cos x\ne0\right)\),
ký hiệu là \(y=\tan x\).
- Vì \(\cos x\ne0\) khi và chỉ khi \(x\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\) nên tập xác định của hàm số \(y=\tan x\) là \(D=R\)/\(\left\{\dfrac{\pi}{2}+k\pi,k\in Z\right\}\).
d) Hàm số côtang
Hàm số côtang là hàm số được xác định bởi công thức :
\(y=\dfrac{\cos x}{\sin x},\left(\sin x\ne0\right)\),
ký hiệu là \(y=\cot x\).
- Vì \(\sin x\ne0\) khi và chỉ khi \(x\ne k\pi\left(k\in Z\right)\) nên tập xác định của hàm số \(y=\cot x\) là
\(D=R\)/\(\left\{k\pi,k\in Z\right\}\).
Nhận xét: Hàm số \(y=\sin x\) là hàm số lẻ, hàm số \(y=\cos x\) là hàm số chẵn.
Từ đó suy ra các hàm số \(y=\tan x\) và \(y=\cot x\) đều là những hàm số lẻ.
2. Tính tuần hoàn của hàm số lượng giác
Người ta chứng minh được rằng \(T=2\pi\) là số dương nhỏ nhất thoả mãn đẳng thức
\(\sin\left(x+T\right)=\sin x,\forall x\in R\)
Hàm số \(y=\sin x\) thoả mãn đẳng thức trên được gọi là hàm số tuần hoàn với chu kì \(2\pi\).
Tương tự, hàm số \(y=\cos x\) là hàm số tuần hoàn với chu kì \(2\pi\).
Các hàm số \(y=\tan x\) và \(y=\cot x\) cũng là các hàm số tuần hoàn với chu kì \(\pi\).
3. Sự biến thiên và đồ thị của hàm số lượng giác
a) Hàm số \(y=\sin x\)
Từ định nghĩa ta thấy hàm số \(y=\sin x\):
- Xác định với mọi \(x\in R\) và \(-1\le\sin x\le1\) ;
- Là hàm số lẻ ;
- Là hàm số tuần hoàn với chu kì \(2\pi\).
- Sự biến thiên và đồ thị hàm số \(y=\sin x\) trên đoạn \(\left[0;\pi\right]\)
Hàm số \(\left[0;\pi\right]\) đồng biến trên \(\left[0;\pi\right]\) và nghịch biến trên
Bảng biến thiên:
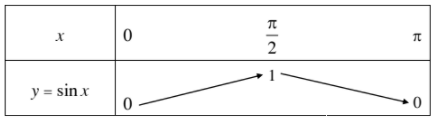
Đồ thị hàm số \(y=\sin x\) trên đoạn \(\left[0;\pi\right]\) đi qua các điểm \(\left(0;0\right)\), \(\left(\dfrac{\pi}{2};1\right)\) và \(\left(\pi;0\right)\).
Chú ý: Vì hàm số \(y=\sin x\) là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn \(\left[0;\pi\right]\) qua gốc toạ độ \(O\) ta được đồ thị hàm số trên đoạn \(\left[-\pi;0\right]\).
Đồ thị hàm số \(y=\sin x\) trên đoạn \(\left[-\pi;\pi\right]\) được biểu diễn như sau:
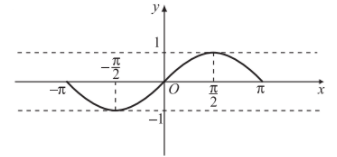
- Đồ thị hàm số \(y=\sin x\) trên \(R\)
Hàm số \(y=\sin x\) là hàm số tuần hoàn chu kì \(2\pi\) nên với mọi \(x\in R\) ta có:
\(\sin\left(x+k2\pi\right)=\sin x,k\in Z\)
Do đó muốn có đồ thị hàm số \(y=\sin x\) trên \(R\) ta tịnh tiến liên tiếp đồ thị hàm số trên đoạn \(\left[-\pi;\pi\right]\) song song với trục hoành từng đoạn có độ dài \(2\pi\).
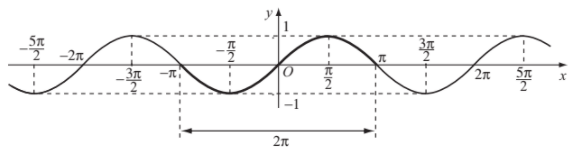
- Tập giá trị của hàm số \(y=\sin x\)
Từ đồ thị ta rút ra kết luận: Tập giá trị của hàm số \(y=\sin x\) là \(\left[-1;1\right]\).
b) Hàm số \(y=\cos x\)
Từ định nghĩa ta thấy hàm số \(y=\cos x\):
- Xác định với mọi \(x\in R\) và \(-1\le\cos x\le1\) ;
- Là hàm số chẵn ;
- Là hàm số tuần hoàn với chu kì \(2\pi\).
Với mọi \(x\in R\) ta có đẳng thức: \(\sin\left(x+\dfrac{\pi}{2}\right)=\cos x\).
Từ đó, bằng cách tịnh tiến đồ thị hàm số \(y=\sin x\) sang trái một đoạn có độ dài bằng \(\dfrac{\pi}{2}\) và song song với trục hoành, ta được đồ thị hàm số \(y=\cos x\):
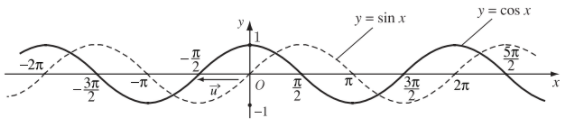
Từ đồ thị hàm số trên ta suy ra:
Hàm số \(y=\cos x\) đồng biến trên đoạn \(\left[-\pi;0\right]\) và nghịch biến trên đoạn \(\left[0;\pi\right]\).
Bảng biến thiên:
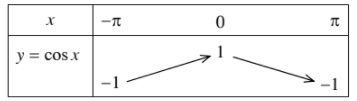
Tập giá trị của hàm số \(y=\cos x\) là \(\left[-1;1\right]\).
Đồ thị của các hàm số \(y=\sin x\), \(y=\cos x\) được gọi chung là các đường hình sin.
c) Hàm số \(y=\tan x\)
Từ định nghĩa ta thấy hàm số \(y=\tan x\):
- Có tập xác định là \(D=R\)\\(\left\{\dfrac{\pi}{2}+k\pi,k\in Z\right\}\) ;
- Là hàm số lẻ ;
- Là hàm số tuần hoàn với chu kì \(\pi\).
- Sự biến thiên và đồ thị hàm số \(y=\tan x\) trên nửa khoảng \([0;\dfrac{\pi}{2})\)
Nhận xét: Hàm số \(y=\tan x\) đồng biến trên nửa khoảng \([0;\dfrac{\pi}{2})\).
Bảng biến thiên:
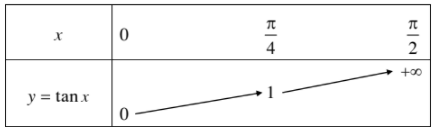
Đồ thị hàm số \(y=\tan x\) trên nửa khoảng \([0;\dfrac{\pi}{2})\) :
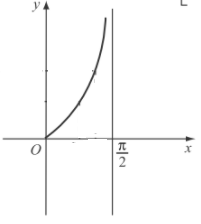
- Đồ thị hàm số \(y=\tan x\) trên \(D\)
Vì hàm số \(y=\tan x\) là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc toạ độ \(O\).
Từ đó ta được đồ thị hàm số \(y=\tan x\) trên khoảng \(\left(-\dfrac{\pi}{2};\dfrac{\pi}{2}\right)\):
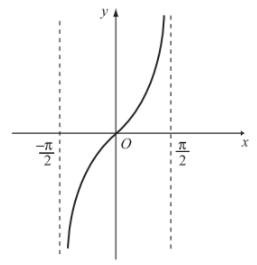
Vì hàm số \(y=\tan x\) tuần hoàn với chu kì \(\pi\) nên tịnh tiến đồ thị hàm số \(y=\tan x\) trên khoảng \(\left(-\dfrac{\pi}{2};\dfrac{\pi}{2}\right)\) song song với trục hoành từng đoạn có độ dài \(\pi\) ta được đồ thị hàm số \(y=\tan x\) trên \(D\):
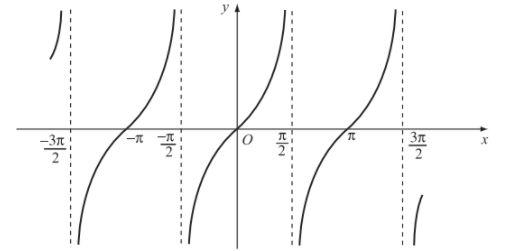
Tập giá trị của hàm số \(y=\tan x\) là khoảng \(\left(-\infty;+\infty\right)\).
4. Hàm số \(y=\cot x\)
Từ định nghĩa ta thấy hàm số \(y=\cot x\) :
- Có tập xác định là \(D=R\backslash\left\{k\pi;k\in Z\right\}\) ;
- Là hàm số lẻ ;
- Làm hàm số tuần hoàn với chu kì \(\pi\).
- Sự biến thiên và đồ thị hàm số \(y=\cot x\) trên khoảng \(\left(0;\pi\right)\)
Nhận xét: Hàm số \(y=\cot x\) nghịch biến trên khoảng \(\left(0;\pi\right)\)
Bảng biến thiên:
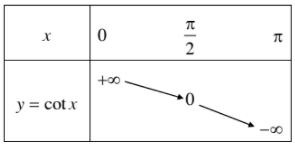
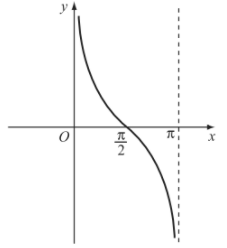
Đồ thị hàm số \(y=\cot x\) trên khoảng \(\left(0;\pi\right)\):
- Đồ thị hàm số \(y=\cot x\) trên \(D\)
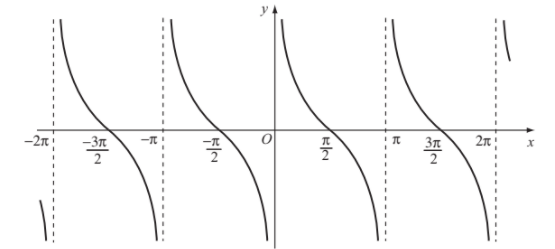
Tập giá trị của hàm số \(y=\cot x\) là khoảng \(\left(-\infty;+\infty\right)\).
@2019450@
II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1. Phương trình \(\sin x=a\)
Xét phương trình \(\sin x=a\) (1)
Trường hợp \(\left|a\right|>1\): Phương trình (1) vô nghiệm, vì \(\left|\sin x\right|\le1\) với mọi \(x\).
Trường hợp \(\left|a\right|\le1\):
Vẽ đường tròn lượng giác tâm \(O\), trục hoành là trục côsin, trục tung là trục sin. Trên trục sin lấy điểm K sao cho \(\overline{OM}=a\). Từ K kẻ các đường vuông góc với trục sin, cắt đường tròn lượng giác tại M và M' đối xứng nhau qua trục sin (Nếu \(\left|a\right|=1\) thì M trùng với M').
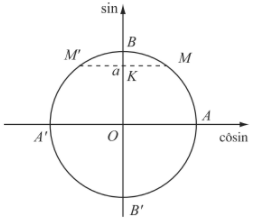
Từ đó ta thấy số đo các cung lượng giác AM và AM' là tất cả các nghiệm của phương trình (1). Gọi \(\alpha\) là số đo bằng radian của một cung lượng giác AM.
Vậy phương trình \(\sin x=a\) có các nghiệm là:
\(x=\alpha+k2\pi,k\in Z\) ;
\(x=\pi-\alpha+k2\pi,k\in Z\).
Nếu số thực \(\alpha\) thoả mãn điều kiện \(\left\{{}\begin{matrix}-\dfrac{\pi}{2}\le\alpha\le\dfrac{\pi}{2}\\\sin\alpha=a\end{matrix}\right.\) thì ta viết \(a=arc\sin\alpha\).
Khi đó các nghiệm của phương trình \(\sin x=a\) được viết là
\(x=arc\sin\alpha+k2\pi,k\in Z\)
và \(x=\pi-arc\sin\alpha+k2\pi,k\in Z\).
Chú ý:
a) Phương trình \(\sin x=\sin\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là
\(x=\alpha+k2\pi,k\in Z\) ;
và \(x=\pi-\alpha+k2\pi,k\in Z\).
Tổng quát: \(\sin f\left(x\right)=\sin g\left(x\right)\Leftrightarrow\left[{}\begin{matrix}f\left(x\right)=g\left(x\right)+k2\pi,k\in Z\\f\left(x\right)=\pi-g\left(x\right)+k2\pi,k\in Z\end{matrix}\right.\).
b) Phương trình \(\sin x=\sin\beta^o\) có các nghiệm là
\(x=\beta^o+k360^o,k\in Z\) ;
và \(x=180^o-\beta^o+k360^o,k\in Z\).
c) Trong một công thức về nghiệm của phương trình lượng giác không được dùng đồng thời hai đơn vị độ và radian.
d) Các trường hợp đặc biệt:
+ \(a=1\): Phương trình \(\sin x=1\) có các nghiệm là \(x=\dfrac{\pi}{2}+k2\pi,k\in Z\).
+ \(a=-1\): Phương trình \(\sin x=-1\) có các nghiệm là \(x=-\dfrac{\pi}{2}+k2\pi,k\in Z\).
+ \(a=0\): Phương trình \(\sin x=0\) có các nghiệm là \(x=k\pi,k\in Z\).
2. Phương trình \(\cos x=a\)
Trường hợp \(\left|a\right|>1\): Phương trình \(\cos x=a\) vô nghiệm vì \(\left|\cos x\right|\le1\) với mọi \(x\).
Trường hợp \(\left|a\right|\le1\):
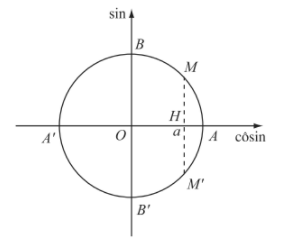
Lấy điểm H trên trục côsin sao cho \(\overline{OH}=a\). Từ H kẻ đường vuông góc với trục côsin, cắt đường tròn lượng giác tại các điểm M và M' đối xứng với nhau qua trục côsin.
Từ đó ta thấy số đo các cung lượng giác AM và AM' là tất cả các nghiệm của phương trình \(\cos x=a\). Gọi \(\alpha\) là số đo bằng radian của một cung lượng giác AM.
Vậy phương trình \(\cos x=a\) có các nghiệm là:
\(x=\pm\alpha+k2\pi,k\in Z\)
Chú ý:
a) Phương trình \(\cos x=\cos\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là
\(x=\pm\alpha+k2\pi,k\in Z\).
Tổng quát: \(\cos f\left(x\right)=\cos g\left(x\right)\Leftrightarrow f\left(x\right)=\pm g\left(x\right)+k2\pi,k\in Z\).
b) Phương trình \(\cos x=\cos\beta^o\) có các nghiệm là
\(x=\pm\beta^o+k360^o,k\in Z\).
c) Nếu số thực \(\alpha\) thoả mãn các điều kiện \(\left\{{}\begin{matrix}0\le\alpha\le\pi\\\cos\alpha=a\end{matrix}\right.\) thì ta viết \(\alpha=arc\cos a\)
Khi đó các nghiệm của phương trình \(\cos x=a\) còn được viết là
\(x=\pm arc\cos a+k2\pi,k\in Z\).
d) Các trường hợp đặc biệt:
+ \(a=1\): Phương trình \(\cos x=1\) có các nghiệm là \(x=k2\pi,k\in Z\).
+ \(a=-1\): Phương trình \(\cos x=-1\) có các nghiệm là \(x=\pi+k2\pi,k\in Z\).
+ \(a=0\): Phương trình \(\cos x=0\) có các nghiệm là \(x=\dfrac{\pi}{2}+k\pi,k\in Z\).
3. Phương trình \(\tan x=a\)
Điều kiện của phương trình là \(x\ne\dfrac{\pi}{2}+k\pi(k\in Z)\).
Khi đó nghiệm của phương trình \(\tan x=a\) là
\(x=arc\tan a+k\pi,k\in Z\).
Chú ý:
a) Phương trình \(\tan x=\tan\alpha\) với \(\alpha\) là một số cho trước có các nghiệm là
\(x=\alpha+k\pi,k\in Z\).
Tổng quát: \(\tan f\left(x\right)=\tan g\left(x\right)\Leftrightarrow f\left(x\right)=g\left(x\right)+k\pi,k\in Z\)
b) Phương trình \(\tan x=\tan\beta^o\) có các nghiệm là
\(x=\beta^o+k180^o,k\in Z\).
4. Phương trình \(\cot x=a\)
Điều kiện của phương trình là \(x\ne k\pi,k\in Z\).
Phương trình \(\cot x=a\) có các nghiệm là
\(x=arc\cot a+k\pi,k\in Z\)
Chú ý:
a) Phương trình \(\cot x=\cot\alpha\), với \(\alpha\) là một số cho trước, có các nghiệm là
\(x=\alpha+k\pi,k\in Z\).
Tổng quát: \(\cot f\left(x\right)=\cot g\left(x\right)\Leftrightarrow f\left(x\right)=g\left(x\right)+k\pi,k\in Z\)
b) Phương trình \(\cot x=\cot\beta^o\) có các nghiệm là
\(x=\beta^o+k180^o,k\in Z\).
Ghi nhớ:
Mỗi phương trình \(\sin x=a\) (\(\left|a\right|\le1\)), \(\cos x=a\) (\(\left|a\right|\le1\)), \(\tan x=a\) (\(\left|a\right|\le1\)) và \(\cot x=a\) (\(\left|a\right|\le1\)) có vô số nghiệm.
Giải các phương trình trên là tìm tất cả các nghiệm của chúng.
@2019535@
III. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
1. Phương trình bậc nhất đối với một hàm số lượng giác
a) Định nghĩa
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng
\(at+b=0\), (1)
trong đó \(a,b\) là các hằng số \(\left(a\ne0\right)\) và \(t\) là một trong các hàm số lượng giác.
b) Cách giải
Chuyển vế rồi chia hai vế của phương trình (1) cho \(a\), ta đưa phương trình (1) về phương trình lượng giác cơ bản.
Ví dụ: Giải phương trình sau: \(3\cos x+5=0\)
Giải:
Từ \(3\cos x+5=0\) chuyển vế ta có: \(3\cos x=-5\) (2)
Chia hai vế của phương trình (2) cho 3, ta được \(\cos x=-\dfrac{5}{3}\)
Vì \(-\dfrac{5}{3}< -1\) nên phương trình đã cho vô nghiệm.
c) Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác
Ví dụ: Giải các phương trình: \(5\cos x-2\sin2x=0\).
Giải:
Ta có \(5\cos x-2\sin2x=0\) \(\Leftrightarrow\) \(5\cos x-4\sin x\cos x=0\) \(\Leftrightarrow\) \(\cos x\left(5-4\sin x\right)=0\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}\cos x=0\\5-4\sin x=0\end{matrix}\right.\)
+ \(\cos x=0\Leftrightarrow\) \(x=\dfrac{\pi}{2}+k\pi,k\in Z\)
+ \(5-4\sin x=0\Leftrightarrow\sin x=\dfrac{5}{4}\). Vì \(\dfrac{5}{4}>1\) nên phương trình này vô nghiệm.
Vậy phương trình (4) có các nghiệm là \(x=\dfrac{\pi}{2}+k\pi,k\in Z\).
2. Phương trình bậc hai đối với một hàm số lượng giác
a) Định nghĩa
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng
\(at^2+bt+c=0\) ,
trong đó \(a,b,c\) là các hằng số (\(a\ne0\)) và \(t\) là một trong các hàm số lượng giác.
b) Cách giải
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có), rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
Ví dụ: Giải phương trình \(2\sin^2\dfrac{x}{2}+\sqrt{2}\sin\dfrac{x}{2}-2=0\).
Giải:
Đặt \(\sin\dfrac{x}{2}=t\) với điều kiện \(-1\le t\le1\) (*)
ta được phương trình bậc hai theo \(t\) là \(2t^2+\sqrt{2}t-2=0\) (1)
Phương trình (1) có hai nghiệm là \(t_1=-\sqrt{2}\) và \(t_2=\dfrac{\sqrt{2}}{2}\) nhưng chỉ có \(t_2=\dfrac{\sqrt{2}}{2}\) thoả mãn điều kiện (*).
Vậy ta có: \(\sin\dfrac{x}{2}=\dfrac{\sqrt{2}}{2}\) \(\Leftrightarrow\) \(\sin\dfrac{x}{2}=\sin\dfrac{\pi}{4}\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}\dfrac{x}{2}=\dfrac{\pi}{4}+k2\pi\\\dfrac{x}{2}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\) \(\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k4\pi\\x=\dfrac{3\pi}{2}+k4\pi\end{matrix}\right.\) (\(k\in Z\))
c) Phương trình đưa về dạng phương trình bậc hai đối với một hàm số lượng giác
Ví dụ: Giải phương trình: \(6\cos^2x+5\sin x-2=0\).
Giải:
Biến đổi \(\cos^2x=1-\sin^2x\) ta đưa phương trình về dạng
\(-6\sin^2x+5\sin x+4=0\)
Đặt \(\sin x=t\) với \(-1\le t\le1\), ta được phương trình bậc hai theo \(t\) là \(-6t^2+5t+4=0\) (3)
Phương trình (3) có hai nghiệm là \(t_1=\dfrac{4}{3}\) và \(t_2=-\dfrac{1}{2}\) nhưng chỉ có nghiệm \(t_2=-\dfrac{1}{2}\) thoả mãn điều kiện.
Vì vậy ta có: \(\sin x=-\dfrac{1}{2}\) \(\Leftrightarrow\) \(\sin x=\sin\left(-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) (\(k\in Z\))
3. Phương trình bậc nhất đối với \(\sin x\) và \(\cos x\)
a) Công thức biến đổi biểu thức \(a\sin x+b\cos x\)
Công thức tổng quát:
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin\left(x+\alpha\right)\) (1)
với \(\cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}}\) và \(\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}}\)
b) Phương trình dạng \(a\sin x+b\cos x=c\)
Xét phương trình \(a\sin x+b\cos x=c\) (2)
với \(a,b,c\in R\), \(a\) và \(b\) không đồng thời bằng 0 (\(a^2+b^2\ne0\))
Nếu \(a=0,b\ne0\) hoặc \(a\ne0,b=0\), phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản. Nếu \(a\ne0,b\ne0\) ta áp dụng công thức (1).
Ví dụ: Giải phương trình: \(\sin x+\sqrt{3}\cos x=1\).
Giải:
Theo công thức (1) ta có:
\(\sin x+\sqrt{3}\cos x=\sqrt{1^2+\left(\sqrt{3}\right)^2}\sin\left(x+\alpha\right)=2\sin\left(x+\alpha\right)\)
trong đó \(\cos\alpha=\dfrac{1}{2}\), \(\sin\alpha=\dfrac{\sqrt{3}}{2}\). Từ đó lấy \(\alpha=\dfrac{\pi}{3}\) thì ta có
\(\sin x+\sqrt{3}\cos x=2\sin\left(x+\dfrac{\pi}{3}\right)\)
Khi đó: \(\sin x+\sqrt{3}\cos x=1\) \(\Leftrightarrow\) \(2\sin\left(x+\dfrac{\pi}{3}\right)=1\) \(\Leftrightarrow\) \(\sin\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\) \(\sin\left(x+\dfrac{\pi}{3}\right)=\sin\dfrac{\pi}{6}\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\x+\dfrac{\pi}{3}=\pi-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\) \(\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\) (\(k\in Z\))
@2019175@