Bài 7: Hình bình hành

1. Định nghĩa

Cho tứ giác \(ABCD\) như hình vẽ sau: 

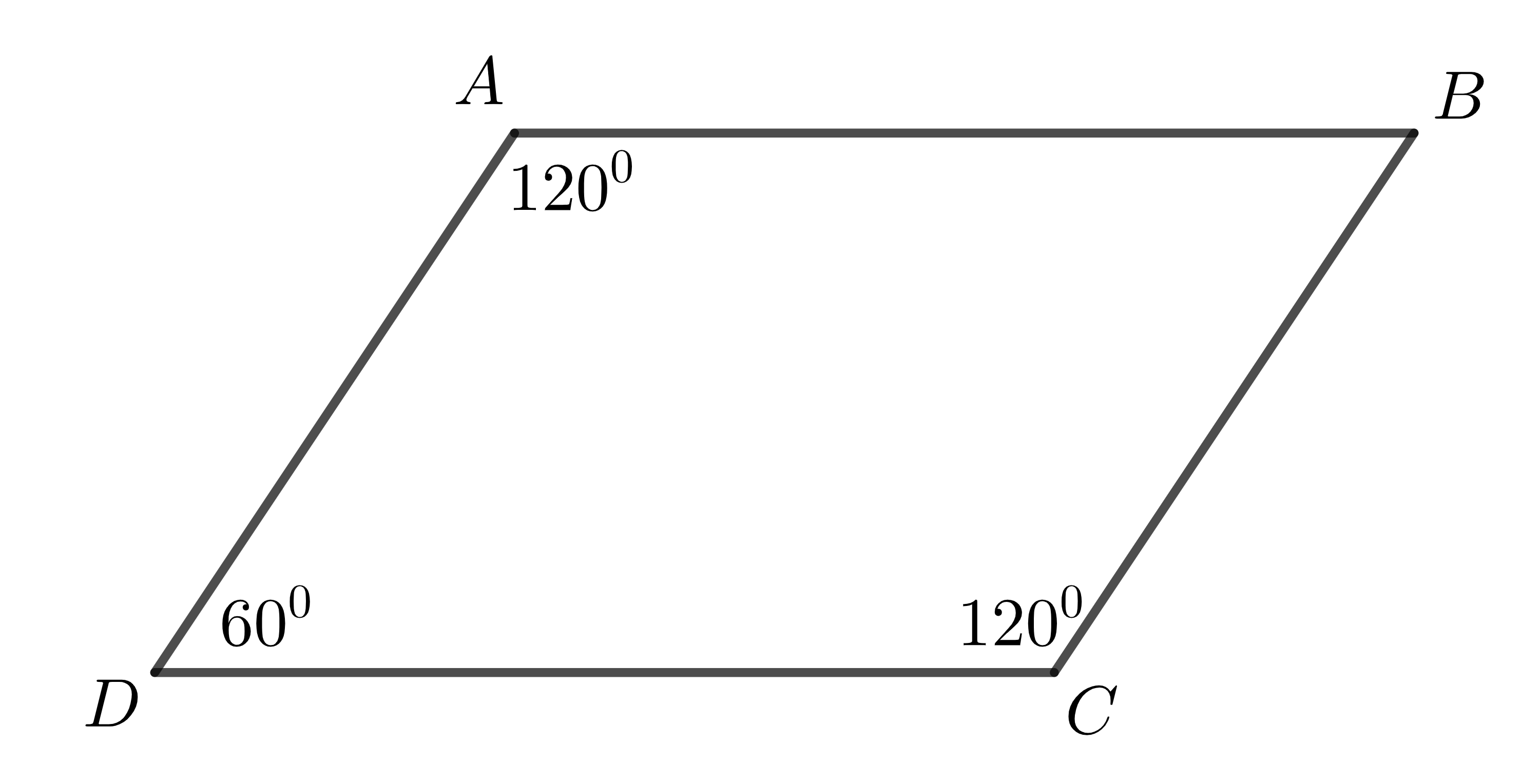
Ta có: \(\widehat{A}+\widehat{D}=180^0\) mà hai góc đồng vị nhau nên \(AB\)//\(CD\). 

Mặt khác: \(\widehat{C}+\widehat{D}=180^0\) mà hai góc đồng vị nhau nên \(AD\)//\(BC\).

Tứ giác \(ABCD\) có các cạnh đối song song với nhau nên ta nói \(ABCD\) là một hình bình hành.

Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song.

\(\text{Tứ giác $ABCD$ là hình bình hành}\Leftrightarrow\{\begin{array} $AB\parallel CD\\ AD\parallel BC \end{array}\)

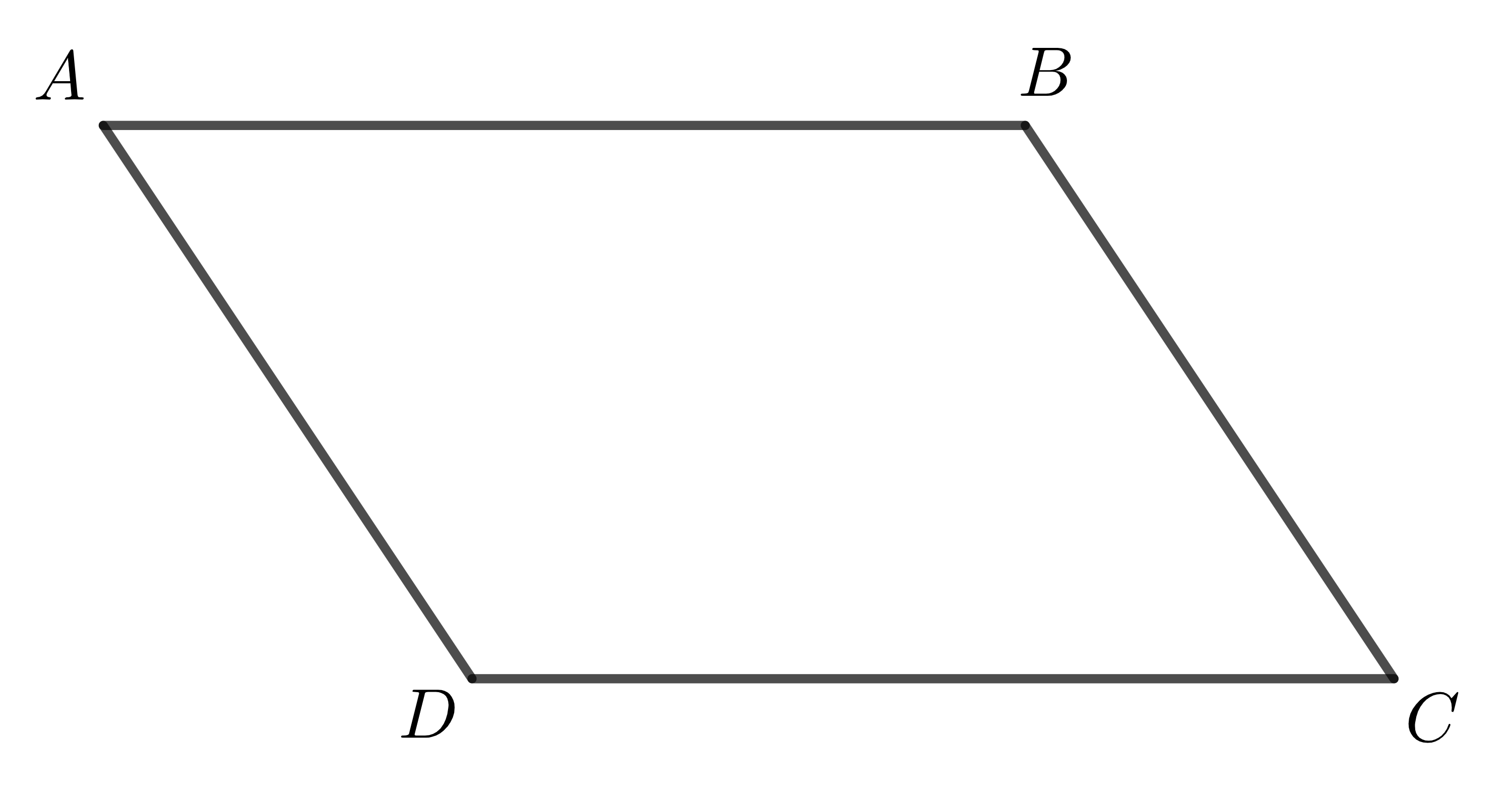
Từ định nghĩa, ta suy ra: Hình bình hành là hình thang đặc biệt (hình thang có hai cạnh bên song song).

2. Tính chất

Các tính chất về cạnh, góc và đường chéo của hình bình hành được phát biểu trong định lí sau:

Định lí: Trong hình bình hành:

• Các cạnh đối bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm mỗi đường.

Chứng minh:

a) Ở trên, ta đã biết: Hình bình hành là hình thang có hai cạnh bên song song. Theo tính chất hình thang, ta suy ra hai cạnh đáy bằng nhau và hai cạnh bên bằng nhau.

Như vậy hình bình hành \(ABCD\) có \(AB=CD,AD=BC\).

b) Ta có hình vẽ: 

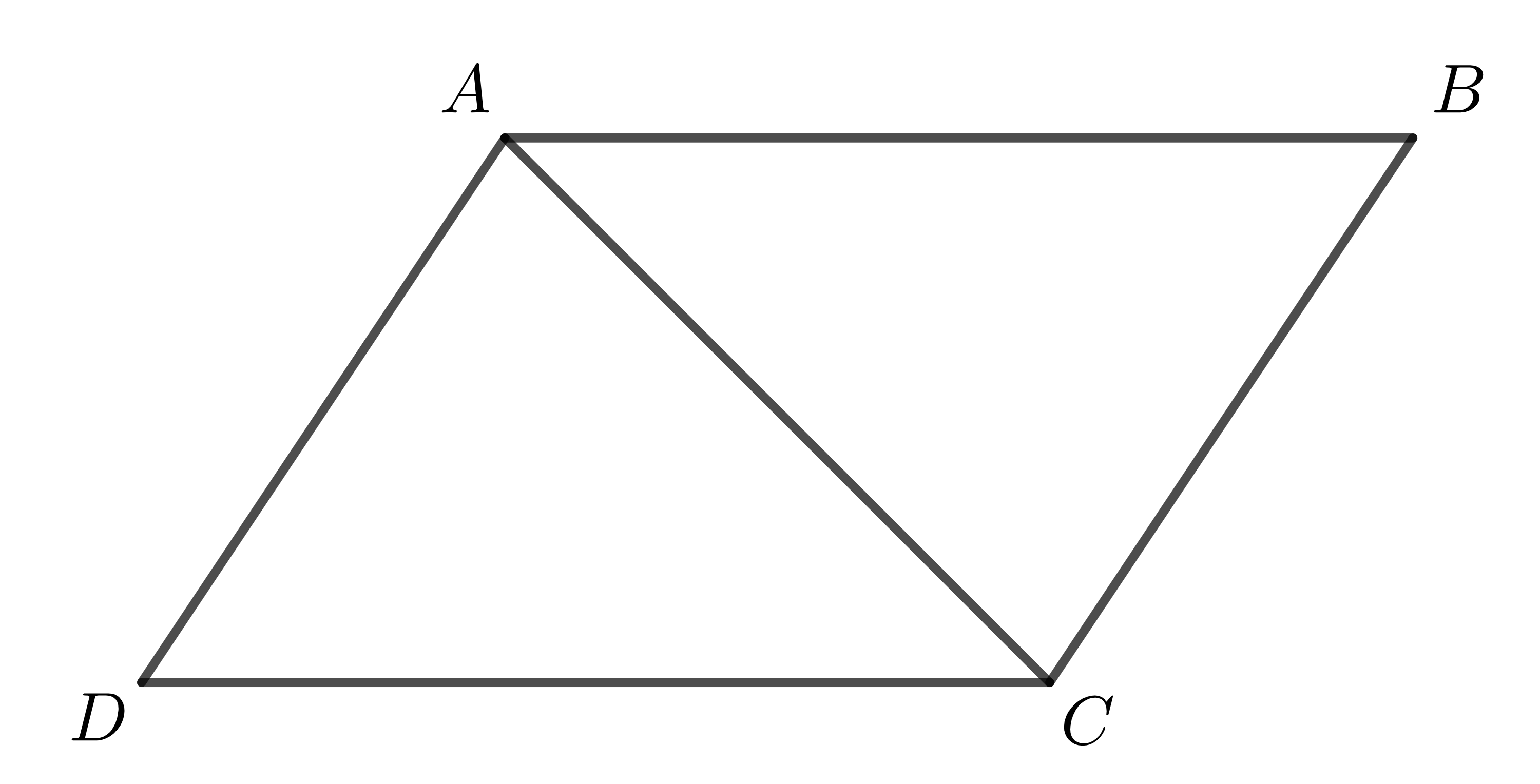
Xét tam giác \(ABC\) và tam giác \(CAD\) có: \(\left\{ \begin{array} $AC \text{ chung}\\AB=CD\\AD=BC \end{array} \right.\) 

\(\Rightarrow\Delta ABC=\Delta CAD\) (cạnh - cạnh - cạnh) \(\Rightarrow\widehat{B}=\widehat{D}\).

Hoàn toàn tương tự, kẻ đường chéo \(BD\) ta chứng minh được: \(\widehat{A}=\widehat{C}\).

c) Gọi \(AC\cap BD\equiv O\).

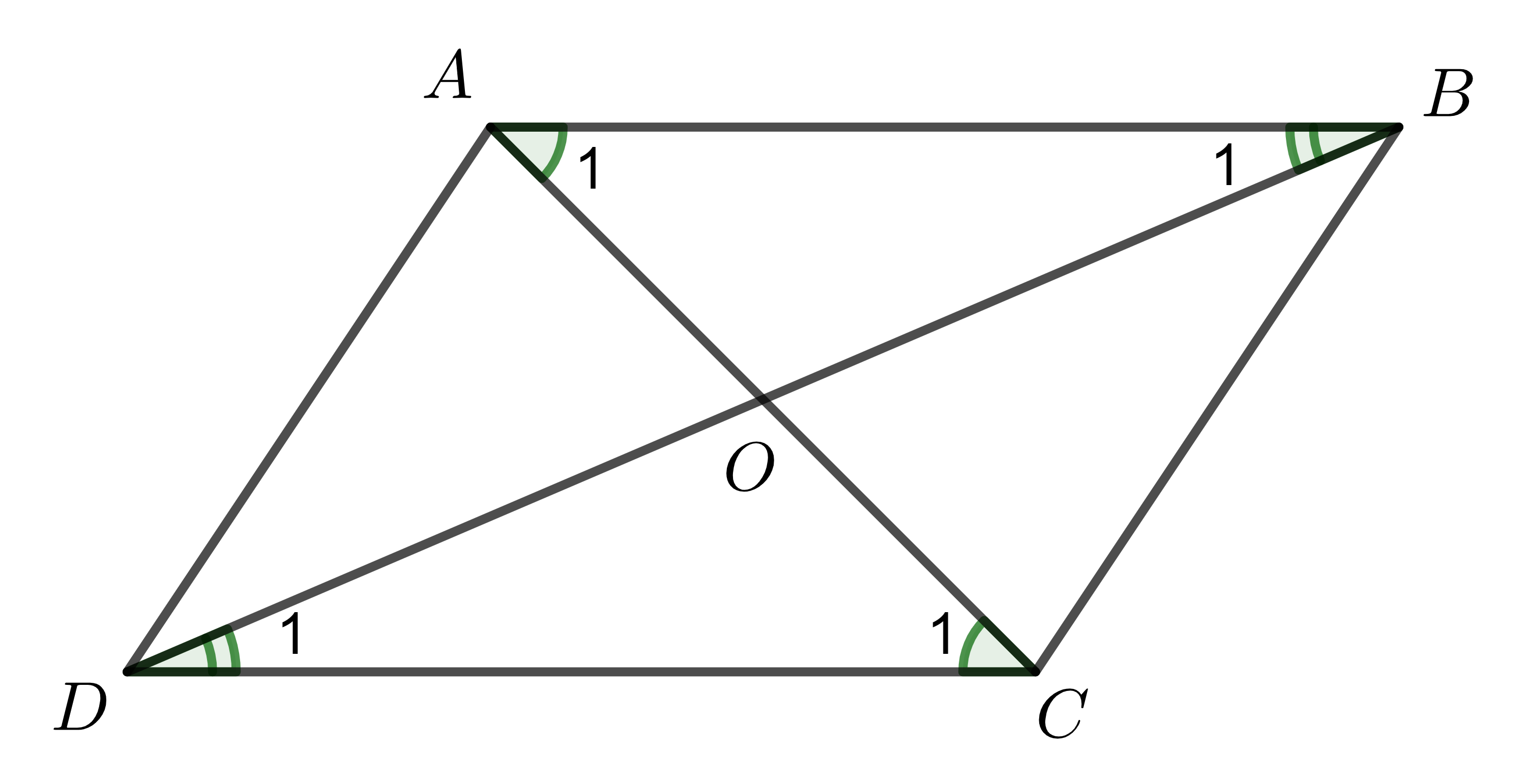
Xét tam giác \(AOB\) và tam giác \(COD\) có: \(\left\{ \begin{array} $\widehat{A_1}=\widehat{C_1} \text{ (so le trong)}\\ AB=CD \\ \widehat{B_1}=\widehat{D_1} \text{ (so le trong)} \end{array}\right.\)

\(\Rightarrow\Delta AOB=\Delta COD\) (góc - cạnh - góc) \(\Rightarrow \left\{ \begin{array} $OA=OB\\ OC=OD \end{array} \right.\).

3. Dấu hiệu nhận biết

Để nhận biết một hình bình hành, ta có các dấu hiệu sau:

1. Tứ giác có các cạnh đối song song là hình bình hành.
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
3. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
4. Tứ giác có các góc đối bằng nhau là hình bình hành.
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Như vậy, để chứng minh một tứ giác là hình bình hành, ta chỉ cần chỉ ra nó thỏa mãn một trong năm dấu hiệu trên.

Ví dụ 1: Cho hình bình hành \(ABCD\). Gọi \(E,F\) lần lượt là trung điểm \(AB,CD\). Chứng minh \(BEDF\) là hình bình hành.

Lời giải:

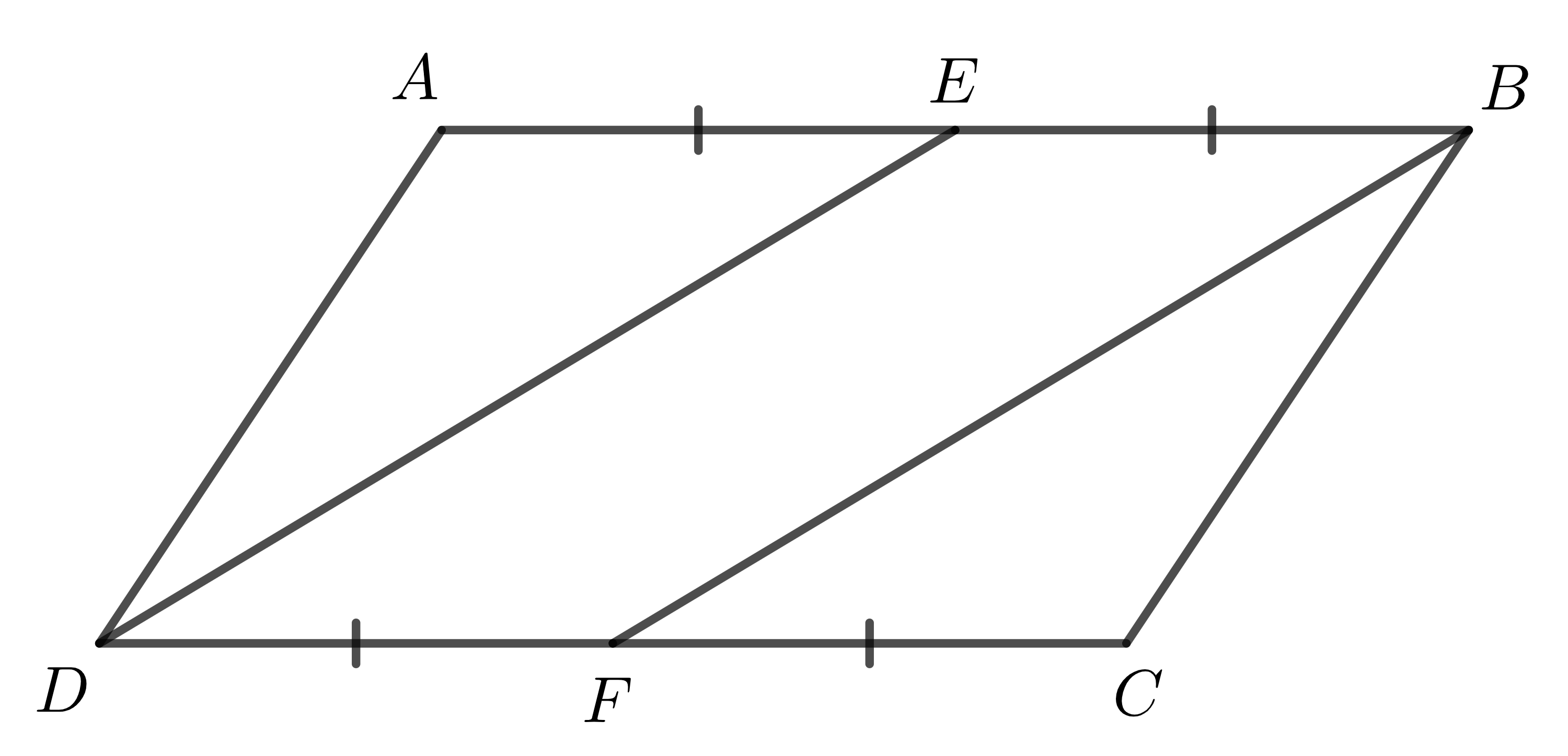
Do \(ABCD\) là hình bình hành \(\Rightarrow \left\{ \begin{array} $AB=CD \\ AB\parallel CD\end{array}\right.\)

\(\Rightarrow \left\{ \begin{array} $\dfrac{1}{2}AB=\dfrac{1}{2}CD \\ EB \parallel DF \end{array} \right.\) \(\Rightarrow \left\{ \begin{array} $EB=DF\\ EB\parallel DF \end{array} \right.\).

Như vậy, tứ giác \(BEDF\) có một cặp cạnh \(BE,DF\) vừa song song vừa bằng nhau

\(\Rightarrow BEDF\) là hình bình hành.

Ví dụ 2: Cho tam giác \(ABC\) có \(H\) là trực tâm. Kẻ các đường thẳng vuông góc với \(AB\) tại \(B\), vuông góc với \(AC\) tại \(C\). Các đường thẳng này cắt nhau tại \(D\). Chứng minh \(BHCD\) là hình bình hành.

Lời giải:

Gọi \(BK,CI\) là các đường cao của tam giác \(ABC\).

Ta có: \(\left\{{}\begin{matrix}BK\perp AC\\CD\perp AC\end{matrix}\right.\left(gt\right)\Rightarrow\) \(BK\)//\(CD\) hay \(BH\)//\(CD\).     (1)

Tương tự: \(\left\{{}\begin{matrix}CI\perp AB\\BD\perp AB\end{matrix}\right.\left(gt\right)\Rightarrow CI\)//\(BD\) hay \(CH\)//\(BD\).       (2)

Từ (1) và (2) \(\Rightarrow BHCD\) là hình bình hành (dấu hiệu 1).