Bài 8: Diện tích xung quanh của hình chóp đều
Nội dung lý thuyết
Các phiên bản khác1. Công thức tính diện tích xung quanh
Diện tích xung quanh của một hình chóp đều là tổng diện tích các mặt bên của hình chóp đều đó.
Ví dụ 1: Xét hình chóp tam giác đều \(A.BCD\):

Diện tích xung quanh của hình chóp tam giác đều \(A.BCD\) được tính bằng tổng diện tích các mặt bên như sau: \(S_{xq}=S_{\Delta ABC}+S_{\Delta ACD}+S_{\Delta ADB}\)
Xét mặt bên \(\Delta SBC\), kẻ đường cao \(SI\) của \(\Delta SBC\) thì \(SI\) chính là trung đoạn của hình chóp tam giác đều \(A.BCD\)
Ta có: \(S_{\Delta ABC}=\dfrac{1}{2}BC.SI\)
Mà \(\Delta ABC=\Delta ACD=\Delta ADB\) nên \(S_{\Delta ABC}=S_{\Delta ACD}=S_{\Delta ADB}\)
Suy ra \(S_{xq}=S_{\Delta ABC}+S_{\Delta ACD}+S_{\Delta ADB}=3.S_{\Delta ABC}=3.\dfrac{1}{2}.BC.SI\)
Mà \(3.BC\) là chu vi tam giác đều \(BCD\)
Ta nhận thấy: Diện tích xung quanh hình chóp tam giác đều \(A.BCD\) được tính là:
\(S_{xq}\) = \(\dfrac{1}{2}\) \(\times\) chu vi đáy \(BCD\) \(\times\) trung đoạn \(SI\)
Ví dụ 2: Xét hình chóp tứ giác đều \(S.ABCD\):

Diện tích xung quanh của hình chóp tứ giác đều \(S.ABCD\) được tính bằng:
\(S_{xq}=S_{\Delta SAB}+S_{\Delta SBC}+S_{\Delta SCD}+S_{\Delta SDA}\)
Xét \(\Delta SCD\) có đường cao \(SI\): \(S_{\Delta SCD}=\dfrac{1}{2}CD.SI\)
Do \(\Delta SAB=\Delta SBC=\Delta SCD=\Delta SDA\)
Nên \(S_{\Delta SAB}=S_{\Delta SBC}=S_{\Delta SCD}=S_{\Delta SDA}\)
Do đó \(S_{xq}=4.S_{\Delta SCD}\)
\(\Rightarrow S_{xq}=4.\dfrac{1}{2}.CD.SI\)
Mặt khác \(4.CD\) chính là chu vi hình vuông \(ABCD\)
Ta nhận thấy: Diện tích xung quanh hình chóp tứ giác đều \(S.ABCD\) được tính là:
\(S_{xq}\) = \(\dfrac{1}{2}\) \(\times\) chu vi đáy \(ABCD\) \(\times\) trung đoạn \(SI\)
Từ đó, ta rút ra công thức:
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
\(S_{xq}=p.d\)
Trong đó: \(p\) là nửa chu vi đáy;
\(d\) là độ dài trung đoạn.
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy.
@1601017@
2. Các ví dụ
Ví dụ 1: Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh bên là \(5cm\), đáy \(ABCD\) là hình vuông cạnh \(6cm\). Tính diện tích toàn phần của hình chóp.
Giải:
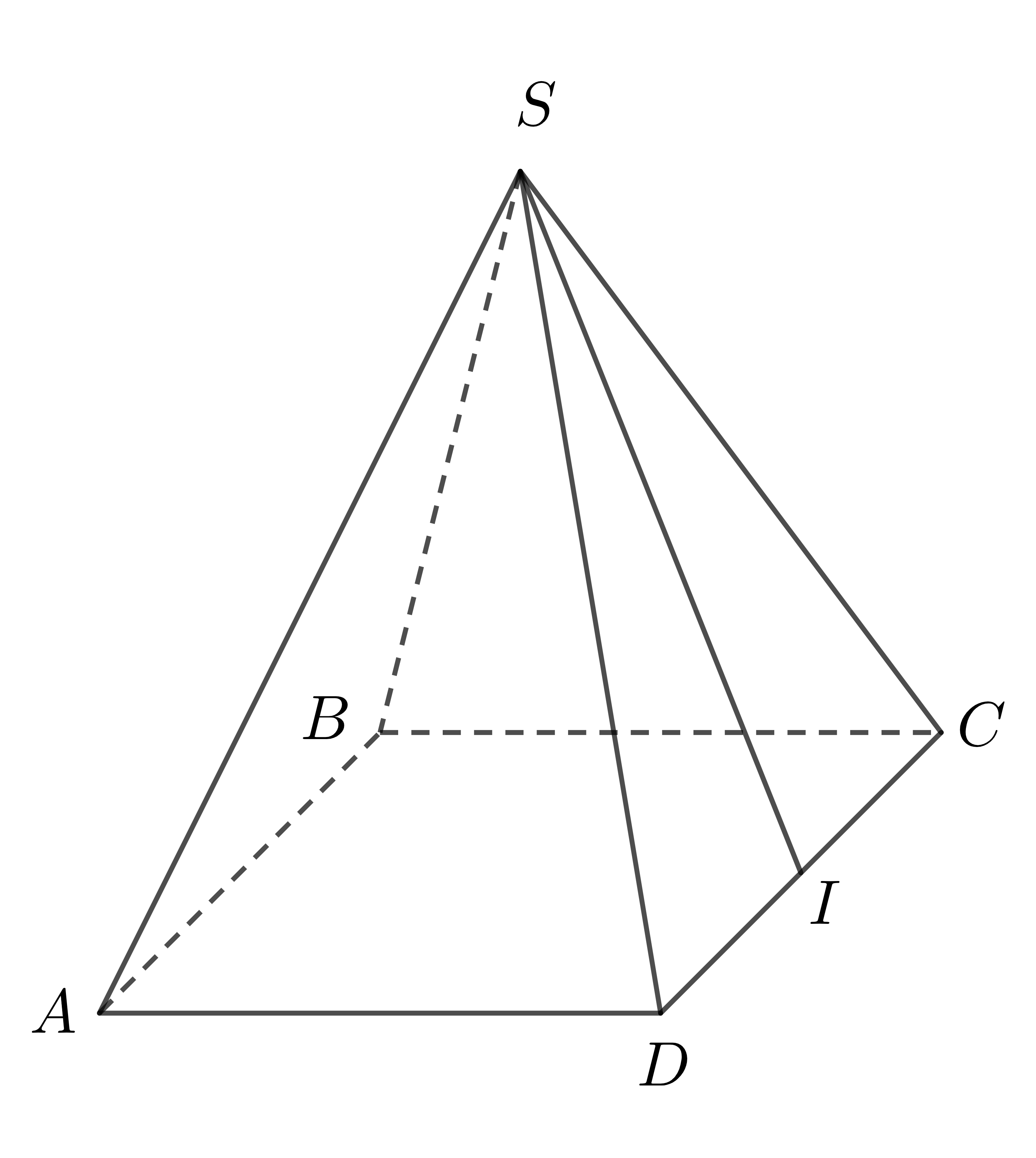
Chu vi đáy \(ABCD\) là: \(6.4=24\left(cm\right)\)
Diện tích đáy \(ABCD\) là: \(S_đ=6.6=36\left(cm^2\right)\)
Kẻ đường cao \(SI\) của tam giác \(SCD\) thì \(SI\) là trung đoạn của hình chóp.
Do \(\Delta SCD\) là tam giác cân tại \(S\) nên đường cao \(SI\) đồng thời là trung tuyến
\(\Rightarrow\) \(I\) là trung điểm \(CD\) \(\Rightarrow\) \(IC=ID=\dfrac{CD}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Xét tam giác \(SID\) vuông tại \(I\). Áp dụng định lí Py-ta-go ta có: \(SI^2+ID^2=SD^2\)
\(\Rightarrow\) \(SI^2+3^2=5^2\) \(\Rightarrow SI=\sqrt{5^2-3^2}=4\left(cm\right)\)
Diện tích xung quanh của hình chóp đều là: \(S_{xq}=\dfrac{24}{2}.4=48\left(cm^2\right)\)
Diện tích toàn phần của hình chóp là: \(S_{tp}=S_{xq}+S_đ=48+36=84\left(cm^2\right)\)
Ví dụ 2: Một hình chóp tứ giác đều có diện tích xung quanh là \(50cm^2\) và độ dài trung đoạn là \(5cm\). Tính độ dài cạnh đáy, cạnh bên và đường cao của hình chóp?
Giải:

Xét hình chóp \(S.ABCD\) có diện tích xung quanh là \(50cm^2\), trung đoạn \(SI=5cm\), đường cao \(SH\).
Áp dụng công thức: \(S_{xq}=p.d\)
\(\Rightarrow50=p.5\) \(\Rightarrow p=10\)
\(\Rightarrow\) Chu vi đáy \(ABCD\) là: \(10.2=20\left(cm\right)\)
\(\Rightarrow\) Độ dài cạnh đáy là: \(\dfrac{20}{4}=5\left(cm\right)\)
Do \(\Delta SCD\) là tam giác cân tại \(S\) nên đường cao \(SI\) đồng thời là trung tuyến \(\Rightarrow IC=ID=\dfrac{CD}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Áp dụng định lí Py-ta-go trong \(\Delta SID\) vuông tại \(I\) ta có \(SI^2+ID^2=SD^2\)
\(\Rightarrow SD=\sqrt{5^2+2,5^2}=\dfrac{5\sqrt{5}}{2}\left(cm\right)\)
Xét trong tam giác \(CAD\) có \(H,I\) là trung điểm \(CA,CD\)
\(\Rightarrow\) \(HI\) là đường trung bình tam giác \(CAD\) \(\Rightarrow HI=\dfrac{1}{2}AD=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Xét tam giác \(SHI\) vuông tại \(H\). Áp dụng định lí Py-ta-go ta có: \(SH^2+HI^2=SI^2\)
\(\Rightarrow SH^2=SI^2-HI^2\)
\(\Rightarrow SH=\sqrt{5^2-2,5^2}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Vậy hình chóp đều \(S.ABCD\) có độ dài cạnh đáy là \(5cm\), cạnh bên là \(\dfrac{5\sqrt{5}}{2}\left(cm\right)\), đường cao là \(\dfrac{5\sqrt{3}}{2}\left(cm\right)\).
Ví dụ 3: Hình chóp \(S.ABC\) có các mặt đều là tam giác đều bằng nhau. \(H\) là tâm đường tròn ngoại tiếp tam giác đều \(ABC\), bán kính \(HC=R=\sqrt{3}\left(cm\right)\). Biết rằng \(AB=R\sqrt{3}\left(cm\right)\). Tính diện tích xung quanh của hình chóp.
Giải:

Dễ thấy \(S.ABC\) là hình chóp tam giác đều.
Bán kính đường tròn ngoại tiếp tam giác đều \(ABC\) là \(R=\sqrt{3}\left(cm\right)\)
Nên \(AB=R.\sqrt{3}=\sqrt{3}.\sqrt{3}=3\left(cm\right)\) hay \(AB=BC=CA=3cm\)
Kẻ đường cao \(SI\) của tam giác \(SBC\) thì \(SI\) là trung đoạn của hình chóp đều
Do \(\Delta SBC\) đều nên \(SI\) cũng là trung tuyến
Do \(BC=3cm\) nên \(IC=\dfrac{3}{2}\left(cm\right)\)
Áp dụng Py-ta-go trong tam giác \(SIC\) vuông tại \(I\) ta tính được \(SI=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
Diện tích xung quanh của hình chóp là: \(S_{xq}=\dfrac{3.3}{2}.\dfrac{3\sqrt{3}}{2}=\dfrac{27\sqrt{3}}{4}\left(cm^2\right)\)
@59971@