Bài 7: Tính chất đường trung trực của một đoạn thẳng
Nội dung lý thuyết
1. Định lí về tính chất của các điểm thuộc đường trung trực
Ta cần nhắc lại định nghĩa: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó.
Ví dụ: Xét đoạn thẳng \(AB\) có trung điểm \(I\). Một đường thẳng \(d\) vuông góc với đoạn thẳng \(AB\) tại \(I\). Khi đó ta gọi đường thẳng \(d\) là trung trực của đoạn thẳng \(AB\).
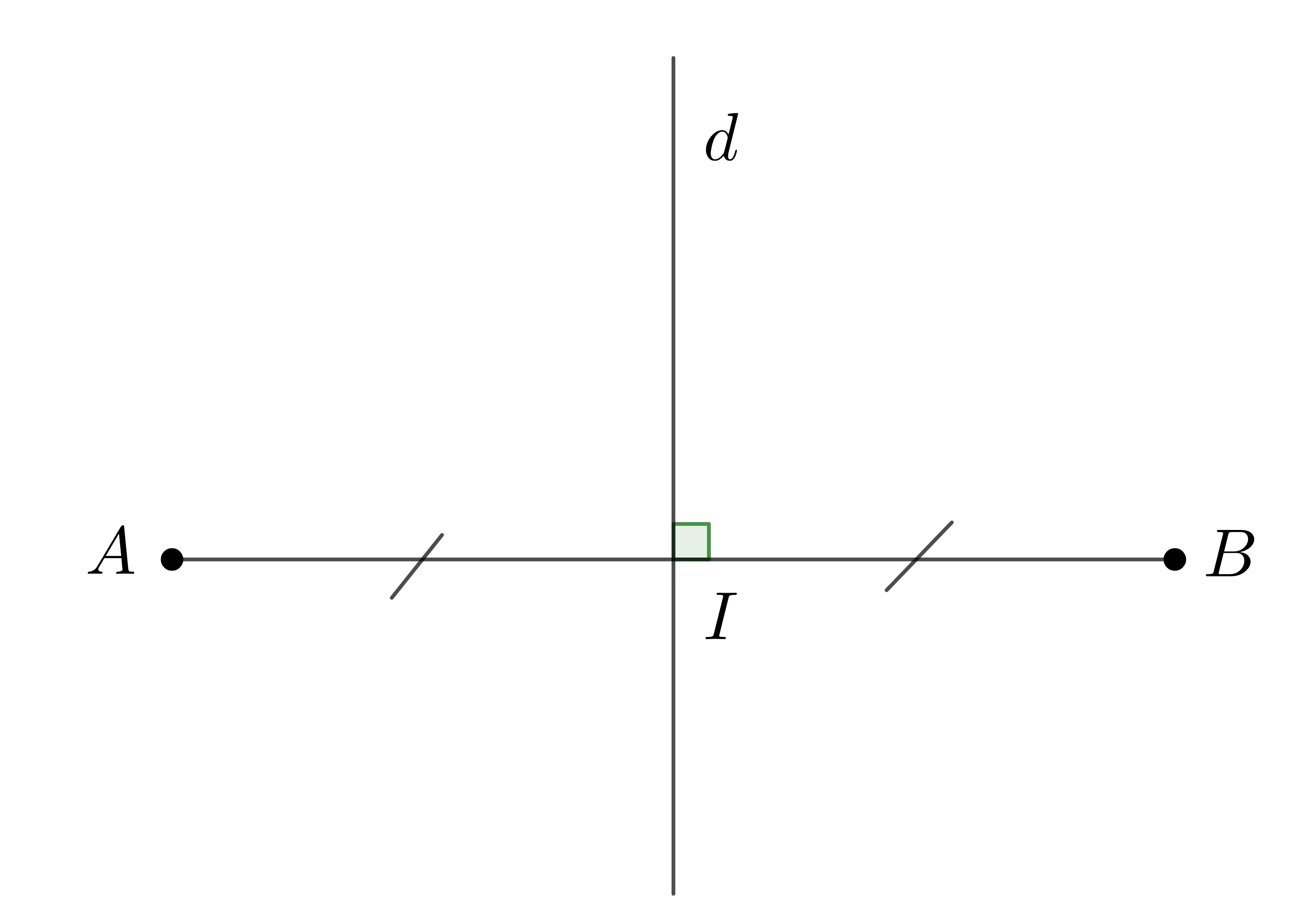
Định lí 1 (định lí thuận):
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ: Điểm M bất kì nằm trên đường trung trực của đoạn thẳng \(AB\) thì ta có \(MA=MB\):
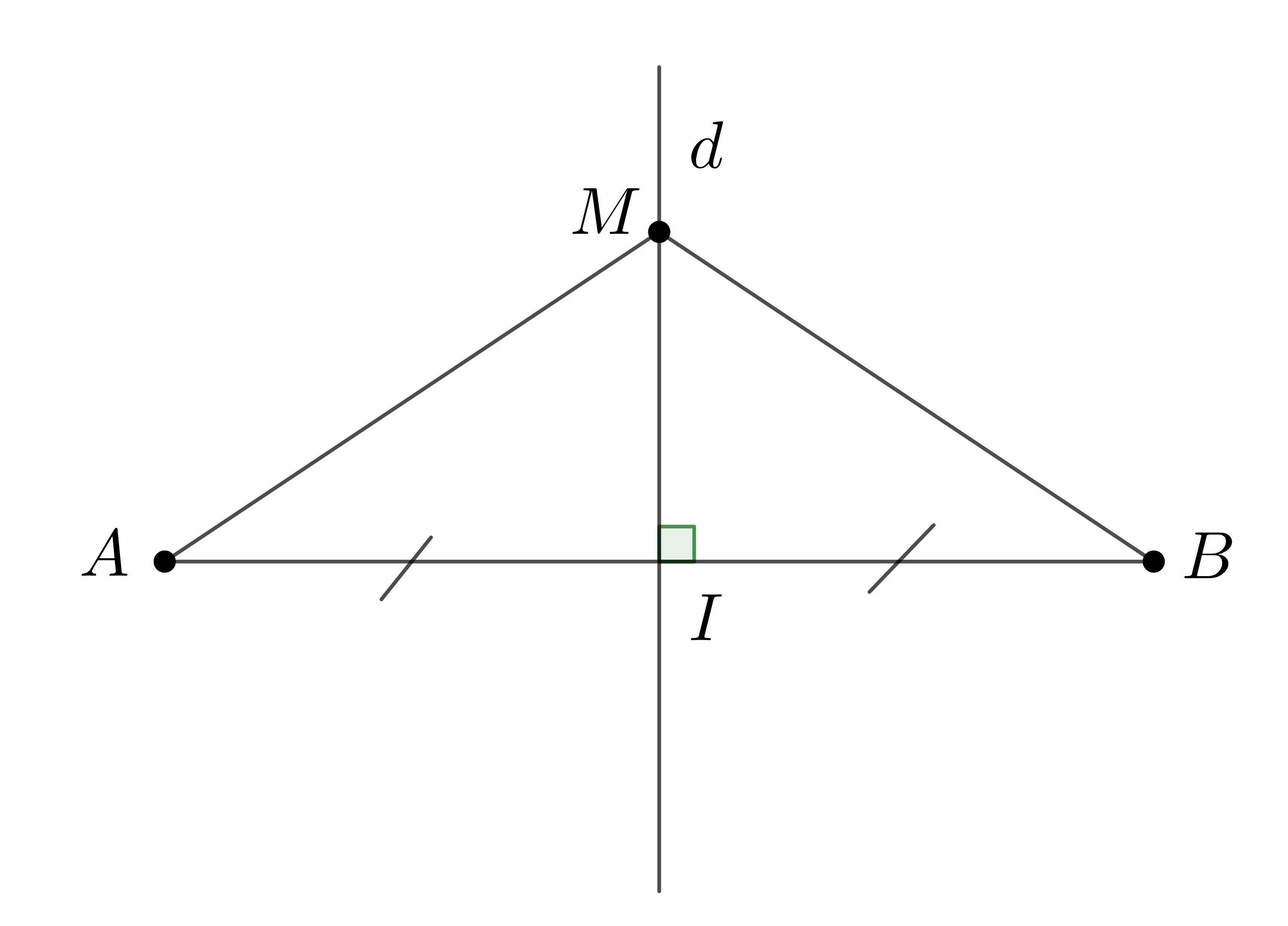
Chứng minh:
Gọi \(I\) là trung điểm của đoạn thẳng \(AB\) thì đường trung trực \(d\) vuông góc với \(AB\) tại \(I\)
Xét \(\Delta MIA\) và \(\Delta MIB\) có:
\(MI\) chung
\(\widehat{MIA}=\widehat{MIB}=90^0\)
\(IA=IB\)
\(\Rightarrow\Delta MIA=\Delta MIB\) (c.g.c)
Suy ra \(MA=MB\) (hai cạnh tương ứng)
Ví dụ 1: Cho \(K\) là một điểm nằm trên đường trung trực của đoạn thẳng \(MN\). Biết độ dài đoạn thẳng \(KM\) là \(7cm\). Tính độ dài đoạn thẳng \(KN\)?
Giải:
Do \(K\) nằm trên đường trung trực của đoạn thẳng \(MN\)
Nên theo định lí 1 ta có: \(KM=KN\)
Mà \(KM=7cm\) suy ra \(KN=7cm\)
Ví dụ 2: Cho 2 điểm \(M,N\) khác nhau cùng nằm trên đường đường trung trực của đoạn thẳng \(AB\). Chứng minh rằng \(\Delta AMN=\Delta BMN\)?
Giải:
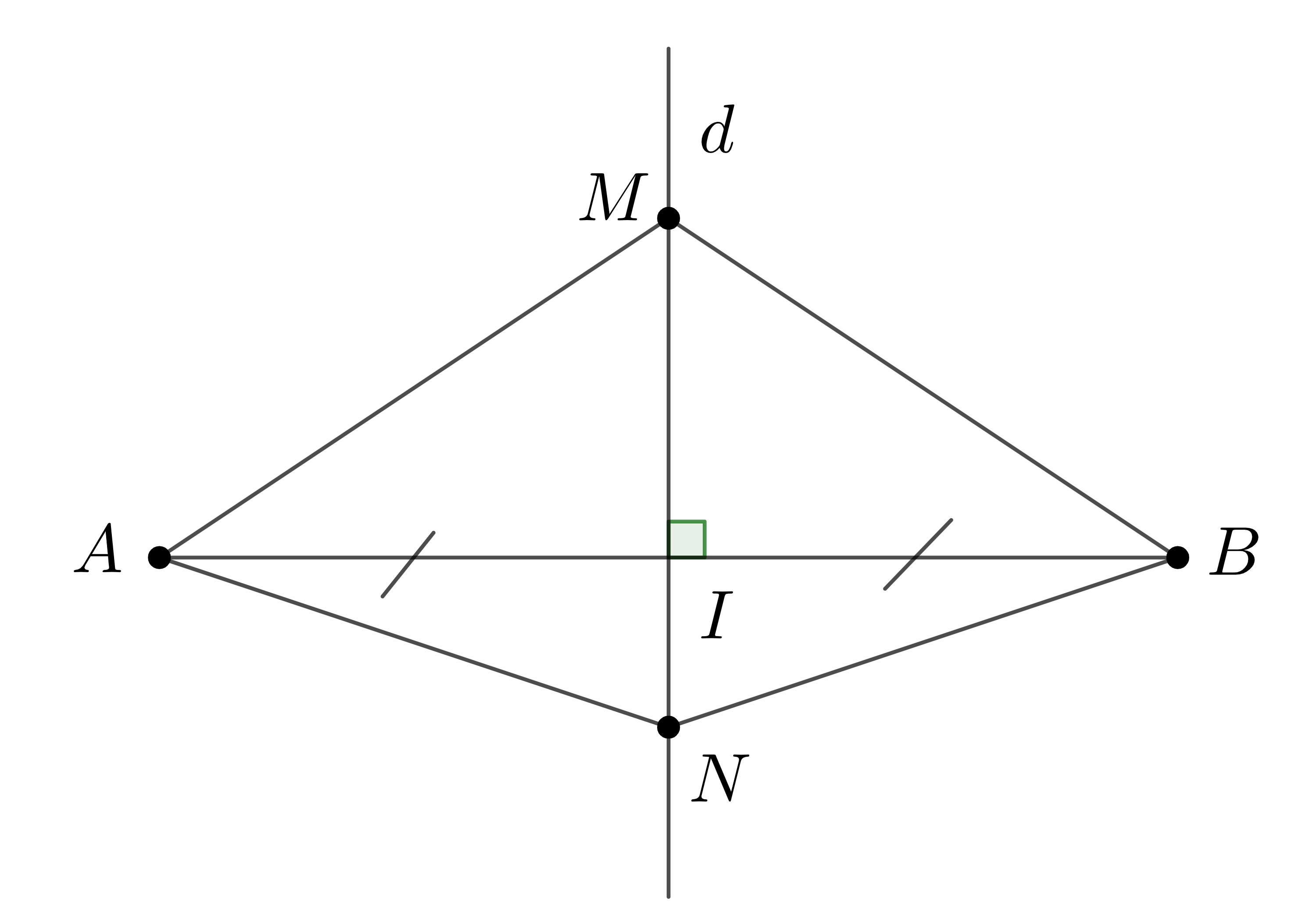
Do \(M\) thuộc trung trực của đoạn thẳng \(AB\) nên theo định lí 1 ta có: \(MA=MB\)
Tương tự, do \(N\) thuộc trung trực của đoạn thẳng \(AB\) nên ta cũng có: \(NA=NB\)
Xét \(\Delta AMN\) và \(\Delta BMN\) có:
\(MA=MB\)
\(NA=NB\)
\(MN\) chung
\(\Rightarrow\Delta AMN=\Delta BMN\) (c.g.c)
@56395@
2. Định lí đảo
Định lí 2 (Định lí đảo):
Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Cụ thể: Nếu \(MA=MB\) thì \(M\) nằm trên đường trung trực của đoạn thẳng \(AB\).
Chứng minh:
Ta xét 2 trường hợp:
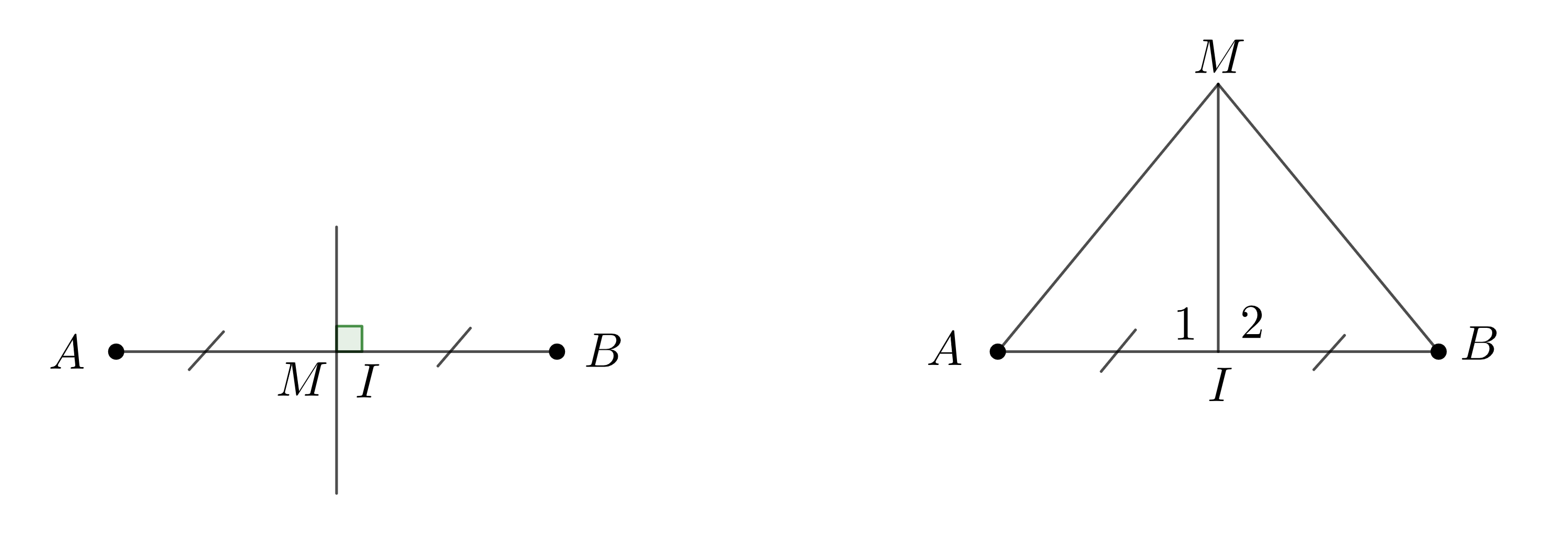
Nếu \(M\in AB\): Vì \(MA=MB\) nên \(M\) là trung điểm của đoạn thẳng \(AB\)
Do đó \(M\) nằm trên đường trung trực của đoạn thẳng \(AB\).
Nếu \(M\notin AB\): Kẻ đoạn thẳng nối \(M\) với trung điểm \(I\) của đoạn thẳng \(AB\).
Ta chứng minh được \(\Delta MIA=\Delta MIB\) (c.c.c)
Suy ra \(\widehat{I_1}=\widehat{I_2}\) (hai góc tương ứng)
Mặt khác: \(\widehat{I_1}+\widehat{I_2}=180^0\)
Nên \(\widehat{I_1}=\widehat{I_2}=90^0\)
Khi đó ta nhận thấy \(MI\) vuông góc với \(AB\) tại trung điểm của nó
Nên \(MI\) là đường trung trực của đoạn thẳng \(AB\).
Nhận xét: Từ Định lí thuận và Định lí đảo ta có:
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Ví dụ 1: Cho các tam giác cân \(ABC\), \(DBC\), \(EBC\) có chung đáy \(BC\).
Chứng minh rằng: các điểm \(A,D,E\) thẳng hàng.
Giải:
Ta có:
Tam giác \(ABC\) cân tại \(A\) \(\Rightarrow AB=AC\)
Tam giác \(DBC\) cân tại \(D\) \(\Rightarrow\) \(DB=DC\)
Tam giác \(EBC\) cân tại \(E\) \(\Rightarrow\) \(EB=EC\)
\(\Rightarrow\)\(A,D,E\) cùng nằm trên đường trung trực của đoạn thẳng \(BC\)
Nên \(A,D,E\) thẳng hàng
@56391@
3. Ứng dụng
Ta có thể vẽ đường trung trực của đoạn thẳng \(MN\) bằng thước và compa như sau:
+) Lấy \(M\) làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}MN\), sau đó lấy \(N\) làm tâm vẽ cung tròn cùng bán kính đó sao cho 2 cung tròn này có hai điểm chung gọi là \(P,Q\).
+) Dùng thước kẻ vẽ đường thẳng \(PQ\), đó chính là đường trung trực của đoạn thẳng \(MN\).
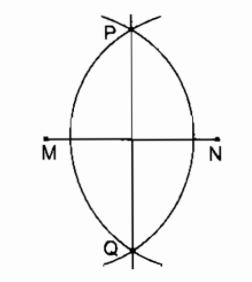
Chú ý:
- Khi vẽ 2 cung tròn trên, ta phải lấy bán kính lớn hơn \(\dfrac{1}{2}MN\) thì 2 cung tròn đó mới có hai điểm chung.
- Giao điểm của đường thẳng \(PQ\) và đoạn thẳng \(MN\) là trung điểm của đoạn thẳng \(MN\)nên cách vẽ trên cũng là cách dựng trung điểm của đoạn thẳng bằng thước và compa.