Bài 5a: Tính lồi lõm và điểm uốn của đồ thị hàm số
Nội dung lý thuyết
Các phiên bản khácI. Khái niệm cung lồi, cung lõm và điểm uốn
Cho đồ thị ACB của hàm số y = f(x) như hình dưới, giả sử đồ thị có tiếp tuyến tại mọi điểm.
Cung lồi: Tại mọi điểm của cung AC, tiếp tuyến luôn nằm bên trên cung, khi đó ta nói cung AC là một cung lồi. Khoảng [a, c] ứng vưới cung lồi AC gọi là khoảng lồi của đồ thị (với a là hoành độ điểm A, c là hoành độ điểm C)
Cung lõm: Trên cung CB, mọi tiếp tuyến đều nằm dưới đồ thị, khi đó CB được gọi là cung lõm và đoạn [c, b] là khoảng lõm của đồ thị.
Điểm uốn: điểm chuyển tiếp giữa cung lồi và cung lõm (từ lồi chuyển sang lõm hoặc từ lõm chuyển sang lồi) gọi là điểm uốn của đồ thị. Điểm C là điểm uốn.
II. Dấu hiệu và cách tìm khoảng lồi, khoảng lõm và điểm uốn
Định lý: Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng (a; b).
- Nếu f''(x) < 0 với mọi \(x\in\left(a;b\right)\) thì đồ thị của hàm số lồi trên khoảng đó
- Nếu f''(x) > 0 với mọi \(x\in\left(a;b\right)\) thì đồ thị của hàm số lõm trên khoảng đó
- Nếu f''(x) đổi dấu khi x đi qua \(x_0\) thì điểm \(M_0\left(x_0;f\left(x_0\right)\right)\) là điểm uốn của đồ thị hàm số
III. Ví dụ
Ví dụ 1: Tìm các khoảng lồi, lõm và điểm uốn của các đồ thị hàm số
a) \(y=x^5\)
b) \(y=-\sin x\) trên đoạn \(\left[0;2\pi\right]\)
Giải:
a) Tập xác định \(\mathbb{R}\), ta có: \(y'=5x^4\); \(y''=20x^3\), bảng xét dấu \(y''\)
Vậy đồ thị hàm số lồi trên \(\left(-\infty;0\right)\), lõm trên khoảng \(\left(0;+\infty\right)\) và điểm (0; 0) là điểm uốn của đồ thị (xem hình vẽ dưới)

b) Ta có \(y'=-\cos x\) ; \(y''=\sin x\), bảng xét dấu \(y''\) trên \(\left(0;2\pi\right)\)
Vậy hàm số \(y=-\sin x\) lõm trên \(\left(0;\frac{\pi}{2}\right)\) , lồi trên \(\left(\frac{\pi}{2};2\pi\right)\). Điểm \(\left(\frac{\pi}{2};0\right)\) là điểm uốn của đồ thị (xem đồ thị phía dưới)

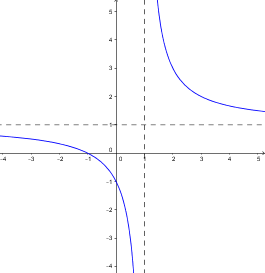
Ví dụ 2: Tìm các khoảng lồi, lõm của đồ thị \(y=\frac{x+1}{x-1}\)
Giải: Tập xác định: \(\mathbb{R}\backslash\left\{1\right\}\)
Ta có: \(y'=-\frac{2}{\left(x-1\right)^2}\) ; \(y'=\frac{4}{\left(x-1\right)^3}\)
Bảng xét dấu của y'':
Đồ thị hàm số lồi trên \(\left(-\infty;1\right)\) và lõm trên \(\left(1;+\infty\right)\) (xem đồ thị phía dưới)